 Подскажите решение, int tg^4 (x/2) dx |
Здравствуйте, гость ( Вход | Регистрация )
| Слаин Артур |
 6.1.2010, 16:55
Сообщение
#1
|
|
Новичок  Группа: Продвинутые Сообщений: 7 Регистрация: 6.1.2010 Из: Пермь Город: Пермь Учебное заведение: ПГИИК  |
Не могу решить никак... (IMG:style_emoticons/default/mellow.gif)
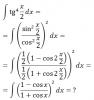 Это ведь через "Новое интегрирование тригонометрических функций" решается? |
   |
 
|
  |
Ответов
| tig81 |
6.1.2010, 17:09
Сообщение
#2
|
|
Академик Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Цитата(Слаин Артур @ 6.1.2010, 18:55)  "Новое интегрирование тригонометрических функций" Что вы под этим подразумеваете? |
|
|
|
| Слаин Артур |
6.1.2010, 17:22
Сообщение
#3
|
|
Новичок Группа: Продвинутые Сообщений: 7 Регистрация: 6.1.2010 Из: Пермь Город: Пермь Учебное заведение: ПГИИК |
Цитата(tig81 @ 6.1.2010, 17:09) Что вы под этим подразумеваете?  Цитата(Ярослав_ @ 6.1.2010, 17:10) Нет, всё проще. tg^4(X)=tg^2(X)*tg^2(X)=tg^2(X)*((1/cos^2(X))-1)=tg^2(X)/cos^2(X)-tg^2(X)=... X=x/2 а с dx что делать? он не заменяется разве? чет я совсем уже запутался... (IMG:style_emoticons/default/bang.gif) |
|
|
|
Сообщений в этой теме
Слаин Артур Подскажите решение 6.1.2010, 16:55
Ярослав_ Нет, всё проще.
tg^4(X)=tg^2(X)*tg^2(X)=tg^2(X)*((... 6.1.2010, 17:10 Ярослав_
Ну хотите, замену сделайте
0.5*x=t
dx=2*dt 6.1.2010, 17:32 Слаин Артур Уфф блин... Вроде че то сделал...
6.1.2010, 19:59 Ярослав_
Колдуй баба, колдуй дед
Трое с боку, ваших нет...... 6.1.2010, 21:00 Слаин Артур (tan/cos) - tan
а это откуда появилось? 7.1.2010, 13:38
граф Монте-Кристо tg^2(x)=(1/cos^2(x))-1. 7.1.2010, 14:01 |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0
|
Текстовая версия | Сейчас: 27.5.2025, 21:40 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru