 Расчёт переходного процесса в цепи с синусоидальным источником. |
Здравствуйте, гость ( Вход | Регистрация )
| MicroMath |
 26.12.2012, 6:06
Сообщение
#1
|
|
Школьник  Группа: Продвинутые Сообщений: 45 Регистрация: 26.12.2012 Город: Россия  |
Добрый день. Прошу помощи в решении задачи. Не могу разобраться, из-за какой ошибки ответы в классическом и операторном методе не сходятся.
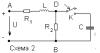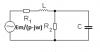  Данные: R1=171 Ом, R2=15 Ом, L=4Гн, C=612 мкФ, Uc(0-)=0, Il(0-)=1.9А, Il(пр)=1.9А, Uc(пр)=28.5 В   Помогите найти ошибку, из-за которой ответы не сходятся.. Заранее благодарен. |
   |
 
|
  |
Ответов(40 - 47)
| MicroMath |
26.12.2012, 19:21
Сообщение
#41
|
|
Школьник Группа: Продвинутые Сообщений: 45 Регистрация: 26.12.2012 Город: Россия |
Цитата(Dimka @ 26.12.2012, 19:16)  Ладно, поскольку мне уже некогда, то вкратце Ток через индуктивность iL(t)=A1*exp(-49.63945938*t)+A2*exp(-102.0430025*t)+1.168474658*sin(62.37878437*t-0.9272664864) При t=0 iL(0)=A1+A2-.9347595827 Напряжение на емкости uc(t) = 27.5578375*A1*exp(-49.63945938*t)+237.1720100*A2*exp(-102.0430025*t) + 1.8732417*sin(62.37878437*t) - 15.0940817*cos(62.37878437*t) При t=0 uc(0)=-15.0940817+27.5578375*A1+237.1720100*A2 До коммутации iL(t)= 1.140696245*sin(62.37878437*t-0.9302163123) iL(0)=-0.9145523486 uc(t)=0, uc(0)=0 Теперь подставляем красные формулы в синие и получаем систему A1+A2-0.9347595827 = -0.9145523486 -15.0940817+27.5578375*A1+237.1720100*A2 = 0, из нее находим A1, A2 A1 = -0.04914501367, A2 = 0.06935224777 Соответственно ток через индуктивность iL(t)= -0.04914501367*exp(-49.63945938*t)+0.06935224777*exp(-102.0430025*t)+0.7011116522*sin(62.37878437*t)-0.9347595827*cos(62.37878437*t) Напряжение на индуктивности найдете по формуле uL(t)=L* iL' (t) А операторный метод. Я вот тут переделал. Проверьте пожалуйста.  Скажите, где я ошибся. |
|
|
|
| Dimka |
26.12.2012, 19:32
Сообщение
#42
|
|
Доцент Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
Некогда вникать
Синусойда в операторной форме e(p)= 22144.46845/(p^2+3891.112739) Дополнительная составляющая ЭДС от индуктивности (сами начертите операторную схему замещения с начальными условиями для индуктивности) eL(p)=L*iL(0)=-3.658209394 Ток через индуктивность iL(p)= [ e(p) + eL(p) ] / (R1+pL + R2 // (1/pC) ) iL(p)= [-0.9145523486*(p+108.9324619)*(p+46.50000005)*(p-46.50000005)] / [ (p+102.0430025)*(p+49.63945934)*(p^2+3891.112741) ] Переходим от изображения к оригиналу (команда invlaplace) и получаем ток iL(p)=0.6935224747*exp(-102.0430025*t)-0.4914501188*exp(-49.63945934*t)-0.9347595842*cos(62.37878438*t)+0.7011116524*sin(62.37878438*t) Он совпадает с током, найденным классическим способом. Вот и всё. (IMG:style_emoticons/default/smile.gif) |
|
|
|
| MicroMath |
26.12.2012, 19:39
Сообщение
#43
|
|
Школьник Группа: Продвинутые Сообщений: 45 Регистрация: 26.12.2012 Город: Россия |
Цитата(Dimka @ 26.12.2012, 19:32) Некогда вникать Синусойда в операторной форме e(p)= 22144.46845/(p^2+3891.112739) Дополнительная составляющая ЭДС от индуктивности (сами начертите операторную схему замещения с начальными условиями для индуктивности) eL(p)=L*iL(0)=-3.658209394 Ток через индуктивность iL(p)= [ e(p) + eL(p) ] / (R1+pL + R2 // (1/pC) ) iL(p)= [-0.9145523486*(p+108.9324619)*(p+46.50000005)*(p-46.50000005)] / [ (p+102.0430025)*(p+49.63945934)*(p^2+3891.112741) ] Переходим от изображения к оригиналу (команда invlaplace) и получаем ток iL(p)=0.6935224747*exp(-102.0430025*t)-0.4914501188*exp(-49.63945934*t)-0.9347595842*cos(62.37878438*t)+0.7011116524*sin(62.37878438*t) Он совпадает с током, найденным классическим способом. Вот и всё. (IMG:style_emoticons/default/smile.gif) Объясните пожалуйста, как это вы определили синусоиду в операторной форме. И ещё, непонятно как то оставлено общее сопротивление. Что то ничего непонятно. Мы так не решали ещё) |
|
|
|
| Dimka |
26.12.2012, 19:44
Сообщение
#44
|
|
Доцент Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
Синусойда
e(t)=355.*sin(62.37878437*t) Теперь по таблицам преобразования найдите изображение этой функции по Лапласу. Я ее искал по команде (laplace) в Маple Сопротивление цепи z(p)= R1+pL+ R2 // (1/pC) Две палочки // означают параллельное сопротивление конденсатора С и резистора R2, т.е. [ R2*(1/pC) ] / [ R2+1/pC ] |
|
|
|
| MicroMath |
26.12.2012, 19:48
Сообщение
#45
|
|
Школьник Группа: Продвинутые Сообщений: 45 Регистрация: 26.12.2012 Город: Россия |
Цитата(Dimka @ 26.12.2012, 19:44) Синусойда e(t)=355.*sin(62.37878437*t) Теперь по таблицам преобразования найдите изображение этой функции по Лапласу. Я ее искал по команде (laplace) в Маple Сопротивление цепи z(p)= R1+pL+ R2 // (1/pC) Две палочки // означают параллельное сопротивление конденсатора С и резистора R2, т.е. [ R2*(1/pC) ] / [ R2+1/pC ] Может всё таки посмотрите мой метод. Он нам как то привычнее и удобнее. |
|
|
|
| Dimka |
26.12.2012, 19:52
Сообщение
#46
|
|
Доцент Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
Ну а что там смотреть? Там отдельные наброски без пояснений.
Если Ваш ответ сойдется с моим (у меня же правильно, т.к. обоими методами одно и тоже получил), то решение верно. Все что мог, я Вам помог. Остальное сами додумывайте. |
|
|
|
| MicroMath |
26.12.2012, 20:02
Сообщение
#47
|
|
Школьник Группа: Продвинутые Сообщений: 45 Регистрация: 26.12.2012 Город: Россия |
Цитата(Dimka @ 26.12.2012, 19:52) Ну а что там смотреть? Там отдельные наброски без пояснений. Если Ваш ответ сойдется с моим (у меня же правильно, т.к. обоими методами одно и тоже получил), то решение верно. Все что мог, я Вам помог. Остальное сами додумывайте. И на том спасибо. |
|
|
|
| MicroMath |
26.12.2012, 20:34
Сообщение
#48
|
|
Школьник Группа: Продвинутые Сообщений: 45 Регистрация: 26.12.2012 Город: Россия |
Цитата(Dimka @ 26.12.2012, 19:52) Ну а что там смотреть? Там отдельные наброски без пояснений. Если Ваш ответ сойдется с моим (у меня же правильно, т.к. обоими методами одно и тоже получил), то решение верно. Все что мог, я Вам помог. Остальное сами додумывайте. Не знаю, операторным что то не получается. По теореме разложения вообще другой ответ выходит. |
|
|
|
|
2 чел. читают эту тему (гостей: 2, скрытых пользователей: 0)
Пользователей: 0
|
Текстовая версия | Сейчас: 25.5.2025, 21:30 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru