Здравствуйте, гость ( Вход | Регистрация )
| Егор66 |
 15.8.2012, 12:42 15.8.2012, 12:42
Сообщение
#1
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 15.8.2012 Город: Екатеринбург Учебное заведение: УРфу Вы: студент |
Всем доброго времени суток. Из за собственной нерадивости приходится самостоятельно осваивать интегрирование. Есть некоторые вопросы возникающие по мере решения, а еще чаще не решения заданий.
Первый вопрос. Есть вот такой интеграл Третий вопрос правильно ли я поступил со следующим выражение |
  |
Ответов(1 - 14)
| Dimka |
 15.8.2012, 15:42 15.8.2012, 15:42
Сообщение
#2
|
|
Доцент       Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
Правильно
|
| Егор66 |
 15.8.2012, 15:58 15.8.2012, 15:58
Сообщение
#3
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 15.8.2012 Город: Екатеринбург Учебное заведение: УРфу Вы: студент |
А что можно сделать со следующим выражением
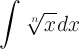 ? Просто довольно часто прихожу к такому интегралу, напрашивается только замена корня на степень 1/n, а далее все по табличной формуле, но ответы получаются не очень красивые, и зачастую не сходятся ? Просто довольно часто прихожу к такому интегралу, напрашивается только замена корня на степень 1/n, а далее все по табличной формуле, но ответы получаются не очень красивые, и зачастую не сходятся |
| venja |
 15.8.2012, 16:04 15.8.2012, 16:04
Сообщение
#4
|
|
Доцент       Группа: Преподаватели Сообщений: 3 615 Регистрация: 27.2.2007 Город: Екатеринбург Вы: преподаватель |
напрашивается только замена корня на степень 1/n, а далее все по табличной формуле, (IMG:style_emoticons/default/yes.gif) |
| Руководитель проекта |
 15.8.2012, 16:16 15.8.2012, 16:16
Сообщение
#5
|
|
Руководитель проекта       Группа: Руководители Сообщений: 3 189 Регистрация: 23.2.2007 Из: Казань Город: Казань Учебное заведение: КГУ Вы: другое |
Егор66, не забывайте про постоянную интегрирования.
Вениамин, а это случайно не ваш студент? (IMG:style_emoticons/default/smile.gif) |
| Егор66 |
 15.8.2012, 16:29 15.8.2012, 16:29
Сообщение
#6
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 15.8.2012 Город: Екатеринбург Учебное заведение: УРфу Вы: студент |
Ну вроде все не так уж и плохо буду разбираться дальше. По поводу постоянной имеется в виду что после ее замены надо будет вернуть изначальное ее значение, или я что не так понял?
|
| Dimka |
 15.8.2012, 16:37 15.8.2012, 16:37
Сообщение
#7
|
|
Доцент       Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
А что можно сделать со следующим выражением 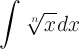 ? Просто довольно часто прихожу к такому интегралу, напрашивается только замена корня на степень 1/n, а далее все по табличной формуле, но ответы получаются не очень красивые, и зачастую не сходятся ? Просто довольно часто прихожу к такому интегралу, напрашивается только замена корня на степень 1/n, а далее все по табличной формуле, но ответы получаются не очень красивые, и зачастую не сходятся=x^(1/n) а дальше интеграл от степенной функции по таблице Егор66, не забывайте про постоянную интегрирования. Вениамин, а это случайно не ваш студент? (IMG:style_emoticons/default/smile.gif) Ну че там с LaTexом решили? Будет? |
| tig81 |
 15.8.2012, 17:20 15.8.2012, 17:20
Сообщение
#8
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
|
| Егор66 |
 15.8.2012, 17:59 15.8.2012, 17:59
Сообщение
#9
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 15.8.2012 Город: Екатеринбург Учебное заведение: УРфу Вы: студент |
А ну да точно куда же без него, спасибо что напомнили)
|
| tig81 |
 15.8.2012, 18:01 15.8.2012, 18:01
Сообщение
#10
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
|
| Руководитель проекта |
 16.8.2012, 4:13 16.8.2012, 4:13
Сообщение
#11
|
|
Руководитель проекта       Группа: Руководители Сообщений: 3 189 Регистрация: 23.2.2007 Из: Казань Город: Казань Учебное заведение: КГУ Вы: другое |
|
| Егор66 |
 18.8.2012, 9:46 18.8.2012, 9:46
Сообщение
#12
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 15.8.2012 Город: Екатеринбург Учебное заведение: УРфу Вы: студент |
В задачнике который у меня на руках сразу после рассмотрения таблицы интегреллов идет ряд заданий под заголовком "Найти первообразную следующих функций." Я к сожалению не очень силен в математической терминологии, хотел спросить в чем состоит смысл данных заданий.
|
| tig81 |
 18.8.2012, 9:55 18.8.2012, 9:55
Сообщение
#13
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
В задачнике который у меня на руках сразу после рассмотрения таблицы интегреллов идет ряд заданий под заголовком "Найти первообразную следующих функций." Я к сожалению не очень силен в математической терминологии, хотел спросить в чем состоит смысл данных заданий. Если в задании задана функция f(x), то надо найти int f(x) dx |
| Егор66 |
 18.8.2012, 10:00 18.8.2012, 10:00
Сообщение
#14
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 15.8.2012 Город: Екатеринбург Учебное заведение: УРфу Вы: студент |
Я так и предпологал, спасибо что уточнили:-)
|
| tig81 |
 18.8.2012, 10:06 18.8.2012, 10:06
Сообщение
#15
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
(IMG:style_emoticons/default/smile.gif) Читайте матчасть (IMG:style_emoticons/default/smile.gif)
|
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 3.8.2025, 10:07 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru









