Здравствуйте, гость ( Вход | Регистрация )
  |
| pmm |
 29.12.2010, 21:41 29.12.2010, 21:41
Сообщение
#1
|
|
Новичок  Группа: Пользователи Сообщений: 1 Регистрация: 29.12.2010 Город: Саранск |
1) С помощью мажоратного признака Вейерштрасса доказать равномерную сходимость функционального ряда в промежутке.
как я понимаю ищется U'n(x), равный и на этом всё) как выразить x через n непонятно.... 2) Исследовать на равномерную сходимость функциональный ряд в промежутке. здесь какой лучше использовать признак? 3) Ну и напоследок, исследовать на сходимость числовой ряд. 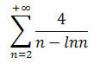 с помощью признаков Раабе, Даламбера у меня не получилось... Может нужно сравнить с каким-либо рядом? Только с каким? |
| Тролль |
 30.12.2010, 6:21 30.12.2010, 6:21
Сообщение
#2
|
|
Доцент       Группа: Преподаватели Сообщений: 2 964 Регистрация: 23.2.2007 Город: Москва Учебное заведение: МГУ |
1. Можно использовать то, что ln (1 + nx) < nx.
А 1/x^n <= 1/a^n. Вот вроде бы и всё. 3. Ряд ведет себя как 4/n. |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 4.8.2025, 10:54 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru








