Версия для печати темы

Нажмите сюда для просмотра этой темы в обычном формате

Образовательный студенческий форум _ Ряды _ Исследование ряда

Автор: pmm 29.12.2010, 21:41

1) С помощью мажоратного признака Вейерштрасса доказать равномерную сходимость функционального ряда в промежутке. Прикрепленное изображение
как я понимаю ищется U'n(x), равный Прикрепленное изображение
и на этом всё) как выразить x через n непонятно....

2) Исследовать на равномерную сходимость функциональный ряд в промежутке. Прикрепленное изображение
здесь какой лучше использовать признак?

3) Ну и напоследок, исследовать на сходимость числовой ряд. 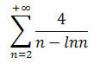Прикрепленное изображение
с помощью признаков Раабе, Даламбера у меня не получилось... Может нужно сравнить с каким-либо рядом? Только с каким?

Автор: Тролль 30.12.2010, 6:21

1. Можно использовать то, что ln (1 + nx) < nx.
А 1/x^n <= 1/a^n. Вот вроде бы и всё.
3. Ряд ведет себя как 4/n.

Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)