Учусь уже на последнем курсе технического университета (но не математический уклон, скорее физический), эту задачу пытаемся и не можем решить уже несколько месяцев (IMG:style_emoticons/default/smile.gif)
Преподаватели могут предложить задачу студентам, она довольно интересна и имеет практическое значение.

Условие:
Есть две одинаковых окружности радиусом R;
эти окружности накладывают друг на друга (см. вложение-картинку).

Задача:
Найти такое расстояние между центрами окружностей X,
при котором площади S будут равны (S1=S2=S3).

Примечания:
Так как окружности одинаковые, то требуется буквенное решение задачи,
т.е. ответом будет уравнение вида X=f( R ).

Желательно привести полное решение, очень интересно каков все-таки результат (IMG:style_emoticons/default/smile.gif)

Первый очевидный вариант

См.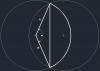

Допустим, что условие равенства площадей выполнено. Тогда очевидно, что площадь выдленного сегмента равна четверти площади круга. Используя формулы площади круга и сегмента (площадь сектора минус площадь треугольника) получаем:

после сокращения получаем:


Учитывая полузабытые правила математики, я не могу выразить отсюда угол "а" в градусной мере (может быть это невозможно, не могу сказать). К тому же величина этого угла позволит лишь подогнать окружности на чертеже к нужному расстоянию, что невозможно на практике.

Что интересно, отсутствие в итоговом уравнении величины радиуса окружности показывает, что выполнение заданного условия возможно при любом размере окружностей и угол "а" при любом радиусе будет постоянным.