Здравствуйте, гость ( Вход | Регистрация )
  |
| N-Talia |
 12.3.2008, 18:45 12.3.2008, 18:45
Сообщение
#1
|
|
Новичок  Группа: Продвинутые Сообщений: 8 Регистрация: 11.3.2008 Город: Stavropol Учебное заведение: STIS URGUES Вы: студент |
Помогите, пжалуйста дорешать (IMG:style_emoticons/default/smile.gif)
А то у меня неясности в некоторых моментах и сказочная дисперсия получается (IMG:style_emoticons/default/newconfus.gif) Условие: Случайная величина Х задана функцией F(x). Найти плостность распределения вероятностей, математическое ожидание М(Х) и дисперсию случайной величины D(Х). F(x)=0, x<=0 F(x)=x^3, 0<x<=1 F(x)=1, x>1 Вообще тут скобочка типа системы уравнений. Решение: 1)Плотностью распределения называют первую производную от функции. f(x)=F'(x)=0, x<0 - Эта не существует значит? f(x)=F'(x)=3x^2, 0<x<=1 f(x)=F'(x)=0, x>1 - И эта не существует? 2) Математическое ожидание: ищем на участке (0;1) M(X)=int от 0 до 1 (x*f(x))dx=int (0;1) (x*3x^2)dx=(после интегрирования получаем)= 3/4=0,75 3)Дисперсия случайной величины: в учебнике есть формула: D(X)=int (а;в) [x-M(X)]^2*f(x)dx Тут квадратные скобки особенные какие-то или обычные? Если они обычные, то есть выражение в скобках надо просто возвести в квадрат, тогда у меня получается: D(X)=int (0;1) ([x-3/4]^2*3x^2)dx=3*int (0;1) (x^4-3/2x^3+9/16)dx интегрируем как сумму интегралов: 3*(int (0;1)(x^4)dx-3/2*int (0;1)(x^3)dx+9/16*int (0;1)dx)=3(1/5*х^5(0;1)-3/2*x^4(0;1)+9/16*x(0;1))= =3(1/5-6+9/16)=-15.7125 (IMG:style_emoticons/default/newconfus.gif) Такое число может быть тут? Дисперсию ищем на отрезке где f(x) не равно нулю? или как то по другой формуле? (IMG:style_emoticons/default/blush.gif) |
| tig81 |
 12.3.2008, 19:16 12.3.2008, 19:16
Сообщение
#2
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
|
| Руководитель проекта |
 13.3.2008, 3:57 13.3.2008, 3:57
Сообщение
#3
|
|
Руководитель проекта       Группа: Руководители Сообщений: 3 189 Регистрация: 23.2.2007 Из: Казань Город: Казань Учебное заведение: КГУ Вы: другое |
Формулу для дисперсии нашли правильную. Надо только внимательнее считать:
D(X)=int (0;1) ([x-3/4]^2*3x^2)dx=3*int (0;1) (x^4-3/2x^3+9/16x^2)dx Дисперсия по определению не может быть отрицательной величиной. Кстати, формула, которую предложила tig81, часто бывает удобнее для вычислений. |
| venja |
 13.3.2008, 4:35 13.3.2008, 4:35
Сообщение
#4
|
|
Доцент       Группа: Преподаватели Сообщений: 3 615 Регистрация: 27.2.2007 Город: Екатеринбург Вы: преподаватель |
f(x)=F'(x)=0, x<0 - Эта не существует значит? f(x)=F'(x)=3x^2, 0<x<=1 f(x)=F'(x)=0, x>1 - И эта не существует? Что значит не существует? А чем Вам 0 не нравится? Просто плотность вероятности f(x) равна 0 вне (0,1). 2) Математическое ожидание: ищем на участке (0;1)M(X)=int от 0 до 1 (x*f(x))dx=int (0;1) (x*3x^2)dx=(после интегрирования получаем)= 3/4=0,75 Вообще-то по определению интеграл от -00 до +00. Но так как f(x) равна 0 вне (0,1), то этот интеграл СВЕДЕТСЯ к интегралу от 0 до 1. Дисперсию ищем на отрезке где f(x) не равно нулю? или как то по другой формуле? (IMG:style_emoticons/default/blush.gif) То же самое замечание. |
| N-Talia |
 13.3.2008, 9:30 13.3.2008, 9:30
Сообщение
#5
|
|
Новичок  Группа: Продвинутые Сообщений: 8 Регистрация: 11.3.2008 Город: Stavropol Учебное заведение: STIS URGUES Вы: студент |
Благодарю всех! (IMG:style_emoticons/default/wub.gif)
Вроде разобралась!!! Дисперсия получилась!!! Четная!!! 0,0375 (IMG:style_emoticons/default/yes.gif) (IMG:style_emoticons/default/clap.gif) Для закрепления результатов пара вопросов (IMG:style_emoticons/default/flowers1.gif) Вообще-то по определению интеграл от -00 до +00. Но так как f(x) равна 0 вне (0,1), то этот интеграл СВЕДЕТСЯ к интегралу от 0 до 1. В общем я пишу общие формулы мат.ожидания с интегралом от -00 до +00 и тут же поясняю, что так "как f(x) равна 0 вне (0,1), то этот интеграл СВЕДЕТСЯ к интегралу от 0 до 1" и дальше уже пишу определенный интеграл и решаю, пральна? Также и с дисперсией. А то решить решили (IMG:style_emoticons/default/megalol.gif) а вот теперь грамотно написать, почему я интеграл беру не с бесконечностью а на отрезке... |
| venja |
 13.3.2008, 13:12 13.3.2008, 13:12
Сообщение
#6
|
|
Доцент       Группа: Преподаватели Сообщений: 3 615 Регистрация: 27.2.2007 Город: Екатеринбург Вы: преподаватель |
|
| tig81 |
 14.3.2008, 6:37 14.3.2008, 6:37
Сообщение
#7
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Дисперсия получилась!!! Четная!!! 0,0375 (IMG:style_emoticons/default/yes.gif) (IMG:style_emoticons/default/clap.gif) не четная, а положительная |
| N-Talia |
 14.3.2008, 7:38 14.3.2008, 7:38
Сообщение
#8
|
|
Новичок  Группа: Продвинутые Сообщений: 8 Регистрация: 11.3.2008 Город: Stavropol Учебное заведение: STIS URGUES Вы: студент |
не четная, а положительная Ой, какая разница!!! Главное что задачка решилась!!!!! (IMG:style_emoticons/default/thumbsup.gif) Эт я от радости очепятку сделала (IMG:style_emoticons/default/megalol.gif) Благодарствую :-) (IMG:style_emoticons/default/flowers1.gif) Пошла дальше дорешивать свою контрольную (IMG:style_emoticons/default/rolleyes.gif) |
| Solitude |
 24.3.2008, 2:04 24.3.2008, 2:04
Сообщение
#9
|
|
Новичок  Группа: Пользователи Сообщений: 3 Регистрация: 24.3.2008 Город: Санкт-Петербург Вы: студент |
Не стал отдельную тему создавать... У меня задача с таким же условием. Я пробовал решать, и ответ получился не очень удачным (IMG:style_emoticons/default/smile.gif) Подскажите, пожалуйста, в чем ошибки. Я так подозреваю, что в интегралах (давно я ими не занимался), но не могу понять, что именно не так.
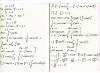 |
| tig81 |
 24.3.2008, 15:30 24.3.2008, 15:30
Сообщение
#10
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Не стал отдельную тему создавать... У меня задача с таким же условием. Я пробовал решать, и ответ получился не очень удачным (IMG:style_emoticons/default/smile.gif) Подскажите, пожалуйста, в чем ошибки. Я так подозреваю, что в интегралах (давно я ими не занимался), но не могу понять, что именно не так. 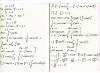 Интеграл для нахождения мат. ожидания: sin(2x)/4(первая строчка на второй страничке).. когда подставляете пределы, то от верхнего предела отнимаем нижний, а у вас два раза знак плюс. Поэтому в ответе при 1/2 другой знак. В дисперсии один раз забыли дописать dx. Когда применяли метод по частям:v=-cos2x/2 и соответственно далее не то подставленно. |
| Solitude |
 24.3.2008, 22:59 24.3.2008, 22:59
Сообщение
#11
|
|
Новичок  Группа: Пользователи Сообщений: 3 Регистрация: 24.3.2008 Город: Санкт-Петербург Вы: студент |
Интеграл для нахождения мат. ожидания: sin(2x)/4(первая строчка на второй страничке).. когда подставляете пределы, то от верхнего предела отнимаем нижний, а у вас два раза знак плюс. Поэтому в ответе при 1/2 другой знак. В дисперсии один раз забыли дописать dx. Когда применяли метод по частям:v=-cos2x/2 и соответственно далее не то подставленно. Спасибо, исправил. Вот так получилось: 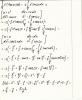 Ответ уже получше вышел (IMG:style_emoticons/default/smile.gif) Теперь все правильно? |
| tig81 |
 25.3.2008, 6:51 25.3.2008, 6:51
Сообщение
#12
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Спасибо, исправил. Вот так получилось: Ответ уже получше вышел (IMG:style_emoticons/default/smile.gif) Теперь все правильно? похоже на правду. В интеграле для мат. ожидания также исправили? |
| Solitude |
 25.3.2008, 15:50 25.3.2008, 15:50
Сообщение
#13
|
|
Новичок  Группа: Пользователи Сообщений: 3 Регистрация: 24.3.2008 Город: Санкт-Петербург Вы: студент |
похоже на правду. В интеграле для мат. ожидания также исправили? Хорошо (IMG:style_emoticons/default/smile.gif) Да, знак исправил. Спасибо Вам большое. |
| tig81 |
 25.3.2008, 17:13 25.3.2008, 17:13
Сообщение
#14
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Пожалуйста. |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 2.8.2025, 17:11 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru









