Здравствуйте, гость ( Вход | Регистрация )
| NecRus |
 26.1.2010, 12:41 26.1.2010, 12:41
Сообщение
#1
|
|
Новичок  Группа: Продвинутые Сообщений: 9 Регистрация: 14.1.2010 Город: Russia Учебное заведение: МАИ Вы: студент |
1ая задача:
Электрическая схема состоит из трех элементов и выходит из строя, если цепь разомкнута (Обрате, пожалуйста, внимания на схему в прикрепленке!) Элементы 1, 2 и 3 независимо друг от друга выходят из строя в течение месяца с вероятностями 0.1, 0.05 и 0.05 соответственно. Определить вероятность безотказной работы схемы в течение месяца. 2ая задача: Настойчивый клиент обходит все ателье в городе, пока не добьется успеха. Найти вероятность того, что ему это удастся с 3 (не ранее) раза, если по статистике среднее число попыток равно 5. Заранее спасибо. (IMG:style_emoticons/default/smile.gif) Эскизы прикрепленных изображений 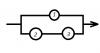
|
  |
Ответов
| Juliya |
 27.1.2010, 11:15 27.1.2010, 11:15
Сообщение
#2
|
|
Старший преподаватель      Группа: Активисты Сообщений: 1 197 Регистрация: 4.11.2008 Город: Москва Вы: преподаватель |
не путайте: термин испытания, проведенные по схеме Бернулли, означает серию повторных независимых испытаний, в каждом из которых некое событие либо происходит с вероятностью р, либо не происходит с вер-тью 1-р.
Схема Бернулли лежит в основе нескольких дискретных распределений, а не только биномиального, вероятности которого рассчитываются по формуле Бернулли и которое Вы как раз и пытались тут изобразить. Отличие биномиального и геометрического в том, что в биномиальном всегда проводится n испытаний, и мы ищем вероятность, что в m из них произошло событие А. А геометрическое представляет собой как раз число испытаний n=m до наступления события А. Как только оно наступает, опыты прекращаются. В Вашей задаче: Настойчивый клиент обходит все ателье в городе, пока не добьется успеха. Как только добьется, он же перестает ходить? А, используя формулу Бернулли, получается что он у вас и дальше пойдет... M(X)=1/p, откуда находите вероятность р, с которой может ожидать успех в каждом ателье. и т.д.. |
Сообщений в этой теме
 NecRus Помогите пожалуйста с задачками 26.1.2010, 12:41
NecRus Помогите пожалуйста с задачками 26.1.2010, 12:41
 tig81 Правила форума
Ваши наработки где? 26.1.2010, 13:54
tig81 Правила форума
Ваши наработки где? 26.1.2010, 13:54
 NecRus Извините, вот наработки:
1 задача.
Рассмотрев схе... 26.1.2010, 18:11
NecRus Извините, вот наработки:
1 задача.
Рассмотрев схе... 26.1.2010, 18:11

 Juliya
Р1 = 0.1+0.05 = 0.15 - вероятность того, что цепь... 26.1.2010, 19:07
Juliya
Р1 = 0.1+0.05 = 0.15 - вероятность того, что цепь... 26.1.2010, 19:07
 NecRus Хм... Получается
Р1= 0.1+0.05-(0.05*0.1)= 0.145
Р2... 26.1.2010, 19:17
NecRus Хм... Получается
Р1= 0.1+0.05-(0.05*0.1)= 0.145
Р2... 26.1.2010, 19:17
 Juliya не понимаете... что Вы ищете-то?
вспомните свою за... 26.1.2010, 20:11
Juliya не понимаете... что Вы ищете-то?
вспомните свою за... 26.1.2010, 20:11
 NecRus Получается, что вероятность безотказной работы сис... 26.1.2010, 20:17
NecRus Получается, что вероятность безотказной работы сис... 26.1.2010, 20:17
 Juliya
2ая задача:
Настойчивый клиент обходит все ателье... 27.1.2010, 10:14
Juliya
2ая задача:
Настойчивый клиент обходит все ателье... 27.1.2010, 10:14
 NecRus А можно поподробней? Если чесно, то ничего не поня... 27.1.2010, 10:28
NecRus А можно поподробней? Если чесно, то ничего не поня... 27.1.2010, 10:28
 Juliya нет, почитайте хоть про геометричесикое распределе... 27.1.2010, 10:55
Juliya нет, почитайте хоть про геометричесикое распределе... 27.1.2010, 10:55
 NecRus Получается так (см. прикрепленку)? 27.1.2010, 11:23
NecRus Получается так (см. прикрепленку)? 27.1.2010, 11:23
 Juliya да, теперь все верно. 27.1.2010, 12:57
Juliya да, теперь все верно. 27.1.2010, 12:57
 NecRus Огромное спасибо, Юлия!
Однако на зачете все р... 27.1.2010, 16:26
NecRus Огромное спасибо, Юлия!
Однако на зачете все р... 27.1.2010, 16:26
 Juliya смотря что подразумевать под k. Если число неудач ... 27.1.2010, 16:36
Juliya смотря что подразумевать под k. Если число неудач ... 27.1.2010, 16:36  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 3.8.2025, 9:02 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru








