Версия для печати темы

Автор: NecRus 26.1.2010, 12:41

1ая задача:

Электрическая схема состоит из трех элементов и выходит из строя, если цепь разомкнута (Обрате, пожалуйста, внимания на схему в прикрепленке!)
Элементы 1, 2 и 3 независимо друг от друга выходят из строя в течение месяца с вероятностями 0.1, 0.05 и 0.05 соответственно.
Определить вероятность безотказной работы схемы в течение месяца.


2ая задача:

Настойчивый клиент обходит все ателье в городе, пока не добьется успеха.
Найти вероятность того, что ему это удастся с 3 (не ранее) раза, если по статистике среднее число попыток равно 5.

Заранее спасибо.


Эскизы прикрепленных изображений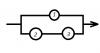

Автор: tig81 26.1.2010, 13:54

http://www.prepody.ru/ipb.html?act=boardrules#
Ваши наработки где?

Автор: NecRus 26.1.2010, 18:11

Извините, вот наработки:

1 задача.
Рассмотрев схему можно увидеть 3 варианта событий, при которых цепи будет разомкнута: 1-2, 1-3, и 1-2-3 эл-ты не работают.
Так же существует вариант когда вся цепь будет работать: 1-2-3 элты работают.

Р1 = 0.1+0.05 = 0.15 - вероятность того, что цепь сломается в эл-тах 1-2.
Р2 = 0.1+0.05 = 0.15 - вероятность для 1-3
Р3 = 0.1 + 0.05 + 0.05 =0.2 - когда все элементы поломаются.

Робщ= Р1+Р2+Р3 = 0.15 + 0.15 + 0.2 = 0.5

Но не может же быть такая огромная вероятнось успешной\неуспешной работы системы! Я никак не могу понять что я не учел и в каком месте применить.

Автор: Juliya 26.1.2010, 19:07

это вероятность, что цепь сломается ИЛИ в 1-м, ИЛИ во 2-м ИЛИ в обоих ( и то, неправильно найдена, т.к. здесь сумма совместных событий.) А то, что написано - это совсем другая операция над событиями - произведение: И первый сломается, И второй...

и т.д.

Автор: NecRus 26.1.2010, 19:17

Хм... Получается
Р1= 0.1+0.05-(0.05*0.1)= 0.145
Р2=0.145
Р3= 0.1 + 0.05 + 0.05 - (0,00025) = 0.199975

Р= 1 - 0,489975 = 0,510025 - ответ

Так получается?

Автор: Juliya 26.1.2010, 20:11

не понимаете... что Вы ищете-то?
вспомните свою задачу:

в каком случае схема будет безотказно работать?
составьте условие её работы, помня, что И в Ваших рассуждениях соответствует произведению событий, а ИЛИ - их сумме.

Р1 = 0.1*0.05 - вероятность того, что цепь сломается в эл-тах и 1, и во 2.
Р2 = 0.1*0.05 - вероятность для 1-3
Р3 = 0.1*0.05*0.05 - когда все элементы поломаются.

Автор: NecRus 26.1.2010, 20:17

Получается, что вероятность безотказной работы системы
Р = 0,98975

Огромное спасибо!

А вторую задачу решать с помощью формулы Бернулли?

Р=(5!/6*(5-3)!)*0.5^3*0.5*2

Так ведь получается?

Т.к. n = 5 (число независимых испытаний)
k = 3 (число наступления данного события)
р = 0.5 (вероятность упеха\неуспеха)

Автор: Juliya 27.1.2010, 10:14

нет, здесь геометрическое распределение - число испытаний, проведенных по схеме Бернулли ДО первого успеха.
Вам дано его матожидание - среднее число попыток равно 5. Через него можно найти вероятность успеха р в одном испытании.
найти надо Р(Х≥3) (если как в условии - не ранее 3-го раза)

Автор: NecRus 27.1.2010, 10:28

А можно поподробней? Если чесно, то ничего не понятно(

Сначала считаем геометрическое распределение, а потом по Бернулли?

Автор: Juliya 27.1.2010, 10:55

нет, почитайте хоть про геометричесикое распределение! Вот http://www.nkzu.kz/NKZU/FIT/mat/ter_ver/geom.htm вроде понятно написано и пример похожий на Ваш...

Автор: Juliya 27.1.2010, 11:15

не путайте: термин испытания, проведенные по схеме Бернулли, означает серию повторных независимых испытаний, в каждом из которых некое событие либо происходит с вероятностью р, либо не происходит с вер-тью 1-р.
Схема Бернулли лежит в основе нескольких дискретных распределений, а не только биномиального, вероятности которого рассчитываются по формуле Бернулли и которое Вы как раз и пытались тут изобразить.

Отличие биномиального и геометрического в том, что в биномиальном всегда проводится n испытаний, и мы ищем вероятность, что в m из них произошло событие А.
А геометрическое представляет собой как раз число испытаний n=m до наступления события А. Как только оно наступает, опыты прекращаются.

В Вашей задаче: Настойчивый клиент обходит все ателье в городе, пока не добьется успеха. Как только добьется, он же перестает ходить? А, используя формулу Бернулли, получается что он у вас и дальше пойдет...

M(X)=1/p, откуда находите вероятность р, с которой может ожидать успех в каждом ателье. и т.д..

Автор: NecRus 27.1.2010, 11:23

Получается так (см. прикрепленку)?


Эскизы прикрепленных изображений

Автор: Juliya 27.1.2010, 12:57

да, теперь все верно.

Автор: NecRus 27.1.2010, 16:26

Огромное спасибо, Юлия!
Однако на зачете все равно пришлось доделать( Оказалось что k больше или равно 3, а не двум(

Автор: Juliya 27.1.2010, 16:36

смотря что подразумевать под k. Если число неудач - Вы все верно сделали. Если число испытаний - тогда да, больше или равно 3.