Здравствуйте, гость ( Вход | Регистрация )
| Talkman |
 1.12.2009, 15:06 1.12.2009, 15:06
Сообщение
#1
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 1.12.2009 Город: Брянск Учебное заведение: БГТУ Вы: студент |
Пожалуйста, помогите найти урaвнeниe кaсaтeльнoй к пoвeрхнoсти x^3y^2z - xz^2 + 2z = 9 в тoчкe (1, -2, 3). насколько я понял первое слагаемое(x^3y^2z) имеет 3хуровневую структуру, так?
Точка не принадлежит поверхности, следовательно нахождение касательной не сводится к использованию формулы F'x (x0, y0, z0) · (x − x0) + F'y (x0, y0, z0) · (y − y0) + F'z (x0, y0, z0) · (z − z0) = 0, правильно? Еще вызвал затруднения вопрос по отысканию частных производных, к примеру при y... Помогите пожалуйста. |
  |
Ответов(1 - 12)
| tig81 |
 1.12.2009, 16:58 1.12.2009, 16:58
Сообщение
#2
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
насколько я понял первое слагаемое(x^3y^2z) имеет 3хуровневую структуру, так? что вы понимаете под термином "трехуровневая структура" Цитата Точка не принадлежит поверхности, почему вы так решили? Цитата Еще вызвал затруднения вопрос по отысканию частных производных, к примеру при y... а при х что получилось? |
| Talkman |
 1.12.2009, 17:32 1.12.2009, 17:32
Сообщение
#3
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 1.12.2009 Город: Брянск Учебное заведение: БГТУ Вы: студент |
1. х в степени 3у, а 3у в степени 2z.
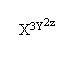 2. Подставил в уравнение координаты точки, получилось неверное равенство. 3.Не уверен, но F'x = x^3y^2z * lnx + z^2 = 4 F'z = x(z^2)' + (2z)' = 2xz + 2 = 8 Насчет же у не знаю, может быть: F'y = 3(y^2z) = 3*y^2z^lny = 3*((-2)^6)*ln(-2). А ведь должно получиться целое нормальное число. Если что - извиняйте - не особо силен... |
| tig81 |
 1.12.2009, 19:17 1.12.2009, 19:17
Сообщение
#4
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
|
| Talkman |
 1.12.2009, 20:02 1.12.2009, 20:02
Сообщение
#5
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 1.12.2009 Город: Брянск Учебное заведение: БГТУ Вы: студент |
то, что у вас было написано изначально, совсем другое выражение.Уточниет условие, там точно не x^3*y^2*z? Условие : x^3y^2z Вы писали : x^3*y^2*z А какая разница-то, кроме игнорирования символа умножения(*), без которого и так все понятно? Вообще, может быть такое условие? Реально ли решить эту задачу? |
| tig81 |
 1.12.2009, 20:22 1.12.2009, 20:22
Сообщение
#6
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Условие : x^3y^2z Вы писали : x^3*y^2*z А какая разница-то, кроме игнорирования символа умножения(*), без которого и так все понятно? большая. Т.к. у вас было записано изначально, то все шло "с игнорированием знака умножения", а после уточнения - уже совершенно иная функция. Т.е. верно записанное условие и правильно расставленные скобки означают очень много. Цитата Вообще, может быть такое условие? А почему бы и нет?! Цитата Реально ли решить эту задачу? Точка в уточненном случае не принадлежит поверхности |
| Talkman |
 1.12.2009, 20:43 1.12.2009, 20:43
Сообщение
#7
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 1.12.2009 Город: Брянск Учебное заведение: БГТУ Вы: студент |
Точка в уточненном случае не принадлежит поверхности т.е. все, если точка не принадлежит поверхности, то написать уравнение касательной к этой поверхности нельзя? Я, конечно, извиняюсь за назойливость, но ответ должен быть 9x - 4y - 17...понятия не имею, как это решить, но, по всей видимости, эта задача решаема. ЗЫ Может быть я что-то где-то кривовато объяснил, тем самым запутав и вас и себя. Исходное задание выглядело так(с точностью до символа): найти уравнение касательной к поверхности x^3y^2z - xz^2 + 2z = 9 в точке (1, -2, 3) |
| граф Монте-Кристо |
 1.12.2009, 20:47 1.12.2009, 20:47
Сообщение
#8
|
|
Доцент       Группа: Преподаватели Сообщений: 3 840 Регистрация: 27.9.2007 Из: Старый Оскол Город: Москва Учебное заведение: МФТИ/МАИ Вы: другое |
Первое слагаемое, видимо, равно (x^3)*(y^2)*(z), а второе - (x)*(z^2). В таком виде точка принадлежит поверхности и всё должно получиться.
|
| tig81 |
 1.12.2009, 21:04 1.12.2009, 21:04
Сообщение
#9
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Первое слагаемое, видимо, равно (x^3)*(y^2)*(z), а второе - (x)*(z^2). В таком виде точка принадлежит поверхности и всё должно получиться. и я о том же, но пост № 3 с другим условием. (IMG:style_emoticons/default/smile.gif) Talkman, откуда взято задание? Сможете сделать скан? |
| граф Монте-Кристо |
 1.12.2009, 21:12 1.12.2009, 21:12
Сообщение
#10
|
|
Доцент       Группа: Преподаватели Сообщений: 3 840 Регистрация: 27.9.2007 Из: Старый Оскол Город: Москва Учебное заведение: МФТИ/МАИ Вы: другое |
Видел. Но, мне всё же кажется,что задание выглядит так как мы с Вами думаем. Потому что иначе очень странно получается (IMG:style_emoticons/default/smile.gif)
|
| tig81 |
 1.12.2009, 21:16 1.12.2009, 21:16
Сообщение
#11
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
угу (IMG:style_emoticons/default/unsure.gif)
|
| Talkman |
 1.12.2009, 22:11 1.12.2009, 22:11
Сообщение
#12
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 1.12.2009 Город: Брянск Учебное заведение: БГТУ Вы: студент |
Спасибо всем, моя ошибка. Как увидел задание, сразу подумал об этой "многоуровневости", хотя на самом деле все очень просто.
|
| tig81 |
 1.12.2009, 22:14 1.12.2009, 22:14
Сообщение
#13
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
|
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 3.8.2025, 22:08 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru









