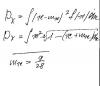Здравствуйте, гость ( Вход | Регистрация )
| OreX |
 27.5.2009, 23:56 27.5.2009, 23:56
Сообщение
#1
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 26.12.2008 Город: Санкт-Петербург Учебное заведение: СПБГИПСР Вы: студент |
|
  |
Ответов(1 - 2)
| Strannick |
 28.5.2009, 5:57 28.5.2009, 5:57
Сообщение
#2
|
|
Студент   Группа: Продвинутые Сообщений: 72 Регистрация: 26.12.2007 Город: Чайковский Вы: студент |
Если проблема с интегралами - то вам в другой раздел.
Интеграл решается через Sudv = uv - Svdu. У вас u = x^2, dv = корень третьей степени() dx. Соответсвенно du = 2xdx, а v= -(3/4)*Корень 3 степени((19/28-x)^4) Затем, с оставшимся интегралом повторить разложение Sudv = uv - Svdu. Определив u=x... смысл, думаю ясен. |
| malkolm |
 28.5.2009, 17:20 28.5.2009, 17:20
Сообщение
#3
|
|
Старший преподаватель      Группа: Преподаватели Сообщений: 2 167 Регистрация: 14.6.2008 Город: Н-ск Вы: преподаватель |
Функция распределения F(x) по плотности находится как интеграл от f(t) в пределах от -оо до x, а Вы интегрируете почему-то по всей прямой. И как может у распределения с плотностью функция распределения оказаться ступенчатой?
Если x взять между 0 и 1, получается F(x) = int[0..x] sqrt[3]{1-t}dt, это и будет функция распределения на этом интервале. Почему-то при вычислении дисперсии Вы плотность поменяли (третий листочек). Да и не нужно этой формулы: дисперсия обычно вычисляется как второй момент минус квадрат первого. |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 3.8.2025, 8:06 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru