Здравствуйте, гость ( Вход | Регистрация )
| Clown |
 25.4.2009, 8:52 25.4.2009, 8:52
Сообщение
#1
|
|
Школьник  Группа: Продвинутые Сообщений: 45 Регистрация: 5.12.2008 Город: Ногинск-9 Учебное заведение: Игумо |
Здравствуйте необходимо найти плащадь фигуры.
y=2/1+x^2 y=x^2 Я построил (см.рисунок)но не могу определит как записать интеграл ограничен он как........ Эскизы прикрепленных изображений 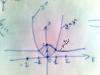
|
  |
Ответов
| Clown |
 25.4.2009, 9:50 25.4.2009, 9:50
Сообщение
#2
|
|
Школьник  Группа: Продвинутые Сообщений: 45 Регистрация: 5.12.2008 Город: Ногинск-9 Учебное заведение: Игумо |
уравнение получается......
х=sqrt[2/(1+x^2)] так...?? будет y=2/(1+x^2) ограниче от 0до2 а y=x^2 ограничена от -1до1 |
| Ярослав_ |
 25.4.2009, 10:10 25.4.2009, 10:10
Сообщение
#3
|
|
Старший преподаватель      Группа: Преподаватели Сообщений: 1 598 Регистрация: 3.1.2008 Город: Тольятти Учебное заведение: УРАО |
Пределы, это те точки, в которых кривые пересекутся. По графику видно, что это точки x1=-1; x2=1,
но т.к. область симметрична относительно оси ОУ, то можно посчитать при x\in [0;1] и результат умножить на два. S=2*int(0;1){[2/(1+x^2)-x^2]dx} уравнение получается...... х=sqrt[2/(1+x^2)] так...?? будет y=2/(1+x^2) ограниче от 0до2 а y=x^2 ограничена от -1до1 x^2=2/(1+x^2); x^2*(1+x^2)=2; x^4+x^2-2=0 ..... (IMG:http://i014.radikal.ru/0904/67/cff87dbf70a6.jpg) |
Сообщений в этой теме
 Clown Найти площадь фигуры 25.4.2009, 8:52
Clown Найти площадь фигуры 25.4.2009, 8:52
 Ярослав_
...но не могу определит как записать интеграл огр... 25.4.2009, 9:09
Ярослав_
...но не могу определит как записать интеграл огр... 25.4.2009, 9:09
 Clown не понимаю))вот уравнение мы прировняли к 0 и что ... 25.4.2009, 10:30
Clown не понимаю))вот уравнение мы прировняли к 0 и что ... 25.4.2009, 10:30
 Ярослав_ Ну написал же...
S=2*int(0;1){[2/(1+x^2)-x^2]dx} 25.4.2009, 10:32
Ярослав_ Ну написал же...
S=2*int(0;1){[2/(1+x^2)-x^2]dx} 25.4.2009, 10:32  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 3.8.2025, 14:36 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru










