Версия для печати темы

Автор: Clown 25.4.2009, 8:52

Здравствуйте необходимо найти плащадь фигуры.
y=2/1+x^2
y=x^2
Я построил (см.рисунок)но не могу определит как записать интеграл ограничен он как........


Эскизы прикрепленных изображений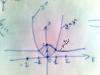

Автор: Ярослав_ 25.4.2009, 9:09

Площадь, которую требуется найти, ограничена сверху кривой y=2/(1+x^2), а снизу y=x^2.
Для того, чтобы найти пределы интегрирования, нужно решить уравнение x^2=2/(1+x^2).
Т.к. обе функции чётные, можно ограничиться условием x>0 и результат удвоить.

Вот более "красивше" график.
http://www.radikal.ru

Автор: Clown 25.4.2009, 9:50

уравнение получается......

х=sqrt[2/(1+x^2)] так...??

будет y=2/(1+x^2) ограниче от 0до2
а y=x^2 ограничена от -1до1

Автор: Ярослав_ 25.4.2009, 10:10

Пределы, это те точки, в которых кривые пересекутся. По графику видно, что это точки x1=-1; x2=1,
но т.к. область симметрична относительно оси ОУ, то можно посчитать при x\in [0;1] и результат умножить на два.
S=2*int(0;1){[2/(1+x^2)-x^2]dx}

x^2=2/(1+x^2);
x^2*(1+x^2)=2;
x^4+x^2-2=0
.....
http://www.radikal.ru

Автор: Clown 25.4.2009, 10:30

не понимаю))вот уравнение мы прировняли к 0 и что дальше....а не можете просто сказать какие пределы интеграла....
какие у y=2/(1+x^2) и y=x^2

Автор: Ярослав_ 25.4.2009, 10:32

Ну написал же...
S=2*int(0;1){[2/(1+x^2)-x^2]dx}