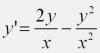x^2y'+y^2-2xy=0 - Образовательный студенческий форум

Здравствуйте, гость ( Вход | Регистрация )

x^2y'+y^2-2xy=0, Найти общее решение дифференциального ур

misha_nick	22.2.2009, 20:03 Сообщение #1
Студент Группа: Продвинутые Сообщений: 53 Регистрация: 16.2.2009 Город: Cheboksary Учебное заведение: MSOU Вы: студент	Задание: Найти общее решение дифференциального уравнения Решение: Делим выражение на x^2 то же самое, что и делаем замену (y/x)=k y=kx y'=k'x+k подставим... Вот что получилось. Чтоб найти общее решение ДУ нужно выразить у через х или просто достаточно будет упростить выражение?

Ответов

misha_nick	22.2.2009, 20:24 Сообщение #2
Студент Группа: Продвинутые Сообщений: 53 Регистрация: 16.2.2009 Город: Cheboksary Учебное заведение: MSOU Вы: студент	Получается так т.е. последнее выражение и есть общее решение? Да?

tig81	22.2.2009, 20:43 Сообщение #3
Академик Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель	Цитата(misha_nick @ 22.2.2009, 22:24) т.е. последнее выражение и есть общее решение? Да? А почему когда домонажали (вторая строка), произвольная константа с не на что не домножилась? Упростите вначале в левой части равенства (привидите к общему знаменателю в знаменателе, сорри за тавтологию) и посмотрите, что можно будет сократить.

Сообщений в этой теме

misha_nick x^2y'+y^2-2xy=0 22.2.2009, 20:03

tig81 Вот что получилось. Чтоб найти общее решение ДУ н... 22.2.2009, 20:17

misha_nick Получается так т.е. последнее выражение и есть о... 22.2.2009, 20:24

tig81 т.е. последнее выражение и есть общее решение? Да... 22.2.2009, 20:43

misha_nick Упростил левую часть А дальше что ? 22.2.2009, 20:51

tig81 Упростил левую часть А дальше что ? Чтобы не моро... 22.2.2009, 20:57

misha_nick Вроде того... 22.2.2009, 21:03

tig81 Вроде того... Либо мы оба ошиблись, либо сделали ... 22.2.2009, 21:10

misha_nick Так и запишем :) Спасибо огромное!!! 22.2.2009, 21:12

tig81 :bigwink: 22.2.2009, 21:16

1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)

Пользователей: 0

Режим отображения: Переключить на: Стандартный · Переключить на: Линейный · Древовидный

Сейчас: 28.5.2025, 2:08

Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.

Зеркало сайта Решебник.Ру - reshebnik.org.ru