Версия для печати темы

Автор: misha_nick 22.2.2009, 20:03

Задание: Найти общее решение дифференциального уравнения

Решение:
Делим выражение на x^2
то же самое, что и
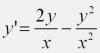
делаем замену (y/x)=k y=kx y'=k'x+k
подставим...


Вот что получилось. Чтоб найти общее решение ДУ нужно выразить у через х или просто достаточно будет упростить выражение?

Автор: tig81 22.2.2009, 20:17

Вроде все верно. Достаточно будет упростить, хотя, по-моему, явно у выразить через х не составит труда.

Автор: misha_nick 22.2.2009, 20:24

Получается так

т.е. последнее выражение и есть общее решение? Да?

Автор: tig81 22.2.2009, 20:43

А почему когда домонажали (вторая строка), произвольная константа с не на что не домножилась?
Упростите вначале в левой части равенства (привидите к общему знаменателю в знаменателе, сорри за тавтологию) и посмотрите, что можно будет сократить.

Автор: misha_nick 22.2.2009, 20:51

Упростил левую часть


А дальше что ?

Автор: tig81 22.2.2009, 20:57

Чтобы не морочить голову, можно так и оставлять. Если же хочется (а хочется ли?) выразить явно у, то домножаем левую и правую часть равенства на (у-х), раскрываем скобки, все, что с у переносим влево и затем его (т.е. у) "красиво" выражаем.

Автор: misha_nick 22.2.2009, 21:03

Вроде того...

Автор: tig81 22.2.2009, 21:10

Либо мы оба ошиблись, либо сделали правильно, вообщем, у меня аналогично получилось.

Автор: misha_nick 22.2.2009, 21:12

Так и запишем

Спасибо огромное!!!

Автор: tig81 22.2.2009, 21:16