Здравствуйте, гость ( Вход | Регистрация )
| infocean |
 17.1.2009, 14:58 17.1.2009, 14:58
Сообщение
#1
|
|
Новичок  Группа: Продвинутые Сообщений: 7 Регистрация: 17.1.2009 Город: Москва |
|
  |
Ответов
| RedNastenka |
 17.1.2009, 16:01 17.1.2009, 16:01
Сообщение
#2
|
|
Студент   Группа: Продвинутые Сообщений: 111 Регистрация: 9.3.2008 Город: Кемерово Учебное заведение: КемГУ Вы: студент |
Здравствуйте! Помогите пожалуйста разобраться с функцией: 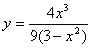 Нашёл производную: 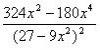 Не могу понять как мне вычислить критические точки? И ещё вопрос: Область определения этой функции от -беск. до +беск? Помогите пожалуйста разобраться,буду очень-очень благодарен! производную нашли неверно, в числителе будет: 324x^2-36x^4=36x^2(9-x^2), знаменатель тот же критические точки будут: х1=0; х2=-3; х3=3; х4=-√3; х5=√3 область определения: (-∞; -√3)U(-√3;√3)U(√3;+∞) вроде так (IMG:style_emoticons/default/smile.gif) |
| infocean |
 17.1.2009, 17:18 17.1.2009, 17:18
Сообщение
#3
|
|
Новичок  Группа: Продвинутые Сообщений: 7 Регистрация: 17.1.2009 Город: Москва |
производную нашли неверно, в числителе будет: 324x^2-36x^4=36x^2(9-x^2), знаменатель тот же критические точки будут: х1=0; х2=-3; х3=3; х4=-√3; х5=√3 область определения: (-∞; -√3)U(-√3;√3)U(√3;+∞) вроде так (IMG:style_emoticons/default/smile.gif) Ого,класс,спасибо большое!!!! (IMG:style_emoticons/default/thumbsup.gif) Подскажите пожалуйста,а по какой формуле надо было вычислять производную,а то я уже совсем запутался,а знать хочется на будущее... Буду супер очень благодарен! (IMG:style_emoticons/default/smile.gif) |
| RedNastenka |
 17.1.2009, 17:20 17.1.2009, 17:20
Сообщение
#4
|
|
Студент   Группа: Продвинутые Сообщений: 111 Регистрация: 9.3.2008 Город: Кемерово Учебное заведение: КемГУ Вы: студент |
Ого,класс,спасибо большое!!!! (IMG:style_emoticons/default/thumbsup.gif) Подскажите пожалуйста,а по какой формуле надо было вычислять производную,а то я уже совсем запутался,а знать хочется на будущее... Буду супер очень благодарен! (IMG:style_emoticons/default/smile.gif) я думаю, вы просто знаком ошиблись при подсчёте, а формула обычная: (u/v)'=(u'*v-u*v')/v^2 |
| infocean |
 17.1.2009, 17:27 17.1.2009, 17:27
Сообщение
#5
|
|
Новичок  Группа: Продвинутые Сообщений: 7 Регистрация: 17.1.2009 Город: Москва |
|
Сообщений в этой теме
 infocean Исследовать функцию у=4x^3/(9*(3-x^2)) 17.1.2009, 14:58
infocean Исследовать функцию у=4x^3/(9*(3-x^2)) 17.1.2009, 14:58
 infocean Помогите плиз высчитать вторую производную,а то у ... 18.1.2009, 22:24
infocean Помогите плиз высчитать вторую производную,а то у ... 18.1.2009, 22:24
 RedNastenka
Помогите плиз высчитать вторую производную,а то у... 19.1.2009, 9:09
RedNastenka
Помогите плиз высчитать вторую производную,а то у... 19.1.2009, 9:09
 infocean
если правильно посчитала вторую производную, то о... 19.1.2009, 9:14
infocean
если правильно посчитала вторую производную, то о... 19.1.2009, 9:14
 RedNastenka
Ок,ещё раз спасибо.
Всё надо бежать, а то опоздаю... 19.1.2009, 9:15
RedNastenka
Ок,ещё раз спасибо.
Всё надо бежать, а то опоздаю... 19.1.2009, 9:15
 infocean
график
Ну всё,теперь я вам по жизни должен,ка... 19.1.2009, 9:18
infocean
график
Ну всё,теперь я вам по жизни должен,ка... 19.1.2009, 9:18
 RedNastenka
Ну всё,теперь я вам по жизни должен,как приеду об... 19.1.2009, 9:22
RedNastenka
Ну всё,теперь я вам по жизни должен,как приеду об... 19.1.2009, 9:22  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 3.8.2025, 12:22 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru











