Здравствуйте, гость ( Вход | Регистрация )
| Рома |
 8.4.2007, 6:08 8.4.2007, 6:08
Сообщение
#1
|
|
Новичок  Группа: Пользователи Сообщений: 3 Регистрация: 8.4.2007 Город: Рязань Учебное заведение: Нет |
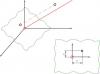 Я с математикой не в ладах. А кому-то, мой вопрос может, покажется простым. Я же, как в стену головой бьюсь. Плоскость проекции проходит через начало координат( но это не принципиально), наклон задает прямая, перпендикулярная плоскости, проходящая под углами к двум осям. Я нашел, только кратчайшее растояние от точки, до прямой. Заданы координаты точки и два угла, все остальные значения можно брать любые. Помогите найти координаты проекции точки, на плоскости, относительно точки пересечения прямой и плоскости. |
  |
Ответов(1 - 6)
| venja |
 8.4.2007, 6:47 8.4.2007, 6:47
Сообщение
#2
|
|
Доцент       Группа: Преподаватели Сообщений: 3 615 Регистрация: 27.2.2007 Город: Екатеринбург Вы: преподаватель |
Я с математикой не в лодах. Да и с русским тоже (IMG:style_emoticons/default/smile.gif) Плоскость проекции проходит через начало координат( но это не принципиально), наклон задает прямая, перпендикулярная плоскости, проходящая под углами к двум осям. Я нашел, только кратчайшее растояние от точки, до прямой. Заданы координаты точки и два угла, все остальные значения можно брать любые. Помогите найти координаты проекции точки, на плоскости, относительно точки пересечения прямой и плоскости. Можно попробовать так (если я правильно понял условие - не ясно, что такое координаты проекции относительно точки пересечения...). 1. Найти направляющий вектор прямой по заданным углам: a={cos(alfa), cos(beta),cos(gama)} . Косинус третьего угла можно найти из условия, что сумма квадратов этих косинусов=1. 2.Записать в параметрическом виде (x=x(t), y=y(t),z=z(t)) уравнение прямой, параллельной данной, и проходящей через проектируемую точку. У этой прямой тот же направляющий вектор. 3. Записать уравнение плоскости (она проходит через начало координат, а за ее нормальный вектор можно взять упоминаемый выше вектор а). 4. Подставить параметрические зависимости x=x(t), y=y(t),z=z(t) в уравнение плоскости и найти решение t полученного уравнения. 5. Подтавить t в x=x(t), y=y(t),z=z(t) и получить координаты проекции. |
| Рома |
 8.4.2007, 9:24 8.4.2007, 9:24
Сообщение
#3
|
|
Новичок  Группа: Пользователи Сообщений: 3 Регистрация: 8.4.2007 Город: Рязань Учебное заведение: Нет |
Допустим так: Я хочу сохранить "снимок" трехмерного объекта. Для этого, мне нужно спроецировать объект на плоскость. И получить две координаты точки, в собственной системы координат плоскости (Xпл, Yпл, Zпл=0(т.к. "снимок"- он плоский)). Лады?
|
| A_nn |
 8.4.2007, 9:47 8.4.2007, 9:47
Сообщение
#4
|
|
Ассистент     Группа: Преподаватели Сообщений: 720 Регистрация: 26.2.2007 Город: СПб Вы: преподаватель |
Тогда так:
1. Берем направляющий вектор прямой, к нему добавляем два ортонормированных вектора, лежащие в плоскости (что-то у меня тут с согласованием падежей...) - получаем базис трехмерного пространства. 2. Находим координаты нужной точки в этом новом базисе. 3. Выкидываем первую из этих координат. |
| Рома |
 8.4.2007, 16:11 8.4.2007, 16:11
Сообщение
#5
|
|
Новичок  Группа: Пользователи Сообщений: 3 Регистрация: 8.4.2007 Город: Рязань Учебное заведение: Нет |
Я-это, только в качестве прикола использовать смогу. Но попробую разобраться. А геометрия, здесь не поможет?
|
| A_nn |
 8.4.2007, 16:50 8.4.2007, 16:50
Сообщение
#6
|
|
Ассистент     Группа: Преподаватели Сообщений: 720 Регистрация: 26.2.2007 Город: СПб Вы: преподаватель |
Это и есть геометрия... аналитическая... (IMG:style_emoticons/default/smile.gif)
А Вам это зачем, если не секрет? |
| Руководитель проекта |
 8.4.2007, 17:25 8.4.2007, 17:25
Сообщение
#7
|
|
Руководитель проекта       Группа: Руководители Сообщений: 3 189 Регистрация: 23.2.2007 Из: Казань Город: Казань Учебное заведение: КГУ Вы: другое |
Это и есть геометрия... аналитическая... (IMG:style_emoticons/default/smile.gif) А Вам это зачем, если не секрет? (IMG:style_emoticons/default/biggrin.gif) |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 4.8.2025, 1:46 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru









