Версия для печати темы

Автор: Рома 8.4.2007, 6:08

Я с математикой не в ладах. А кому-то, мой вопрос может, покажется простым. Я же, как в стену головой бьюсь.

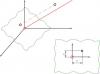
Плоскость проекции проходит через начало координат( но это не принципиально), наклон задает прямая, перпендикулярная плоскости, проходящая под углами к двум осям. Я нашел, только кратчайшее растояние от точки, до прямой. Заданы координаты точки и два угла, все остальные значения можно брать любые.

Помогите найти координаты проекции точки, на плоскости, относительно точки пересечения прямой и плоскости.

Автор: venja 8.4.2007, 6:47

Да и с русским тоже



Можно попробовать так (если я правильно понял условие - не ясно, что такое координаты проекции относительно точки пересечения...).

1. Найти направляющий вектор прямой по заданным углам: a={cos(alfa), cos(beta),cos(gama)} .
Косинус третьего угла можно найти из условия, что сумма квадратов этих косинусов=1.
2.Записать в параметрическом виде (x=x(t), y=y(t),z=z(t)) уравнение прямой, параллельной данной, и проходящей через проектируемую точку. У этой прямой тот же направляющий вектор.
3. Записать уравнение плоскости (она проходит через начало координат, а за ее нормальный вектор можно взять упоминаемый выше вектор а).
4. Подставить параметрические зависимости x=x(t), y=y(t),z=z(t) в уравнение плоскости и найти решение t полученного уравнения.
5. Подтавить t в x=x(t), y=y(t),z=z(t) и получить координаты проекции.

Автор: Рома 8.4.2007, 9:24

Допустим так: Я хочу сохранить "снимок" трехмерного объекта. Для этого, мне нужно спроецировать объект на плоскость. И получить две координаты точки, в собственной системы координат плоскости (Xпл, Yпл, Zпл=0(т.к. "снимок"- он плоский)). Лады?

Автор: A_nn 8.4.2007, 9:47

Тогда так:
1. Берем направляющий вектор прямой, к нему добавляем два ортонормированных вектора, лежащие в плоскости (что-то у меня тут с согласованием падежей...) - получаем базис трехмерного пространства.
2. Находим координаты нужной точки в этом новом базисе.
3. Выкидываем первую из этих координат.

Автор: Рома 8.4.2007, 16:11

Я-это, только в качестве прикола использовать смогу. Но попробую разобраться. А геометрия, здесь не поможет?

Автор: A_nn 8.4.2007, 16:50

Это и есть геометрия... аналитическая...
А Вам это зачем, если не секрет?

Автор: Руководитель проекта 8.4.2007, 17:25