Здравствуйте, гость ( Вход | Регистрация )
  |
| Ollie |
 2.10.2012, 11:25 2.10.2012, 11:25
Сообщение
#1
|
|
Новичок  Группа: Продвинутые Сообщений: 7 Регистрация: 2.10.2012 Город: беларусь Учебное заведение: В Вы: студент |
Приведена схема соединения элементов, образующих
цепь с одним входом и одним выходом. Предполагается, что отказы элементов являются независимыми в совокупности событиями. Отказ любого из элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный элемент. Вероятности отказа элементов 1, 2 соответственно равны p1=0,1; p2=0,2. Найти вероятность того, что сигнал пройдет со входа на выход. Эскизы прикрепленных изображений 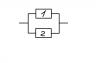
|
| malkolm |
 2.10.2012, 11:44 2.10.2012, 11:44
Сообщение
#2
|
|
Старший преподаватель      Группа: Преподаватели Сообщений: 2 167 Регистрация: 14.6.2008 Город: Н-ск Вы: преподаватель |
Что делали, что не получается?
А где на рисунке элемент 5? |
| Руководитель проекта |
 2.10.2012, 12:08 2.10.2012, 12:08
Сообщение
#3
|
|
Руководитель проекта       Группа: Руководители Сообщений: 3 189 Регистрация: 23.2.2007 Из: Казань Город: Казань Учебное заведение: КГУ Вы: другое |
|
| LADY_I |
 2.10.2012, 12:18 2.10.2012, 12:18
Сообщение
#4
|
|
Новичок  Группа: Пользователи Сообщений: 1 Регистрация: 2.10.2012 Город: Самара Учебное заведение: СГЭУ Вы: студент |
Помогите, пожалуйста, решить!
"Игорь и Михаил получили задание: напечатать по странице некоторого текста. Длительные наблюдения показали, что каждый из них сможет сделать не более одной опечатки на странице текста, причем Игорь может допустить опечатку с вероятностью 0,01, а Михаил - с вероятностью 0,02. Напечатанные страницы попали для проверки редактору, который обнаружил опечатку на одной из страниц. Какова вероятность того, что опечатка сделана Михаилом?" Есть формула Байеса, по которой нужно производить расчеты, есть ответ (99/148). Но мне не совсем понятно, как найти вероятности сразу 2-х страниц, а не одной. |
| Ollie |
 2.10.2012, 12:20 2.10.2012, 12:20
Сообщение
#5
|
|
Новичок  Группа: Продвинутые Сообщений: 7 Регистрация: 2.10.2012 Город: беларусь Учебное заведение: В Вы: студент |
|
| malkolm |
 2.10.2012, 12:23 2.10.2012, 12:23
Сообщение
#6
|
|
Старший преподаватель      Группа: Преподаватели Сообщений: 2 167 Регистрация: 14.6.2008 Город: Н-ск Вы: преподаватель |
|
| Ollie |
 2.10.2012, 12:25 2.10.2012, 12:25
Сообщение
#7
|
|
Новичок  Группа: Продвинутые Сообщений: 7 Регистрация: 2.10.2012 Город: беларусь Учебное заведение: В Вы: студент |
|
| malkolm |
 2.10.2012, 12:28 2.10.2012, 12:28
Сообщение
#8
|
|
Старший преподаватель      Группа: Преподаватели Сообщений: 2 167 Регистрация: 14.6.2008 Город: Н-ск Вы: преподаватель |
Помогите, пожалуйста, решить! "Игорь и Михаил получили задание: напечатать по странице некоторого текста. Длительные наблюдения показали, что каждый из них сможет сделать не более одной опечатки на странице текста, причем Игорь может допустить опечатку с вероятностью 0,01, а Михаил - с вероятностью 0,02. Напечатанные страницы попали для проверки редактору, который обнаружил опечатку на одной из страниц. Какова вероятность того, что опечатка сделана Михаилом?" Есть формула Байеса, по которой нужно производить расчеты, есть ответ (99/148). Но мне не совсем понятно, как найти вероятности сразу 2-х страниц, а не одной. Во-первых, заведите свою тему. В формуле Байеса есть какие-то события. Введите нужные обозначения, гипотезы заведите, событие случившееся опишите через боле простые. Вот всё и станет на место. 2 Ollie: Уже хорошо. Теперь начинайте решать. Не вижу ни одного места, где бы следовало помогать в этой задаче. |
| Ollie |
 2.10.2012, 13:16 2.10.2012, 13:16
Сообщение
#9
|
|
Новичок  Группа: Продвинутые Сообщений: 7 Регистрация: 2.10.2012 Город: беларусь Учебное заведение: В Вы: студент |
Ответ: p(В)=0,98.
|
| malkolm |
 2.10.2012, 16:05 2.10.2012, 16:05
Сообщение
#10
|
|
Старший преподаватель      Группа: Преподаватели Сообщений: 2 167 Регистрация: 14.6.2008 Город: Н-ск Вы: преподаватель |
Ответ верный. Решение показать не хотите? Мы бы его покритиковали.
|
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 3.8.2025, 23:37 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru









