 найти матрицу в базисе |
Здравствуйте, гость ( Вход | Регистрация )
| Rыся |
  15.6.2010, 18:17
Сообщение
#1
|
|
Школьник  Группа: Продвинутые Сообщений: 23 Регистрация: 10.1.2010 Из: Москва Город: Москва  |
Подскажите, пожалуйста, с чего начать:
Эскизы прикрепленных изображений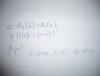 
|
   |
 
|
  |
Ответов
| Rыся |
15.6.2010, 18:34
Сообщение
#2
|
|
Школьник Группа: Продвинутые Сообщений: 23 Регистрация: 10.1.2010 Из: Москва Город: Москва |
Я считаю, нужно сначало найти Ψ(e1), Ψ(e2), Ψ(e3). Получится матрица AΨ(e). Потом Ψ(f1), Ψ(f2), Ψ(f3).
|
|
|
|
| tig81 |
15.6.2010, 18:47
Сообщение
#3
|
|
Академик Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Цитата(Rыся @ 15.6.2010, 21:34)  Я считаю, нужно сначало найти Ψ(e1), Ψ(e2), Ψ(e3). Получится матрица AΨ(e). Что такое е1 и т.д.? Вы работаете в пространстве многочленов. Ищите сразу Цитата Ψ(f1), Ψ(f2), Ψ(f3) |
|
|
|
| Rыся |
15.6.2010, 18:57
Сообщение
#4
|
|
Школьник Группа: Продвинутые Сообщений: 23 Регистрация: 10.1.2010 Из: Москва Город: Москва |
Ψ(f1)=(x+1)*(2+3x)"=0
Ψ(f2)=(x+1)*(x^2)"=2x+2 Ψ(f3)=(x+1)*(x^2+1)"=2x+2 |
|
|
|
Сообщений в этой теме
Rыся найти матрицу в базисе 15.6.2010, 18:17
tig81
Подскажите, пожалуйста, с чего начать:
Вспомнить/... 15.6.2010, 18:19
граф Монте-Кристо Раскладывайте теперь эти векторы по базису. 15.6.2010, 19:16 |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0
|
Текстовая версия | Сейчас: 29.5.2025, 10:09 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru