Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ ТФКП и операционное исчисление _ Вычислить интеграл, используя основную теорему о вычетах
Автор: RaiN17 16.11.2008, 10:21
Вычислить интеграл, используя основную теорему о вычетах...
Если я все правильно понял то тут единственная особая точка z=0
и это полюс первого порядка. Поправьте меня если я ошибаюсь.
Или полюс 4 порядка, вот в этом я запутался... ((( 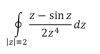
Автор: tig81 16.11.2008, 10:46
Если я все правильно понял то тут единственная особая точка z=0
так
Цитата
и это полюс первого порядка. Поправьте меня если я ошибаюсь.
Или полюс 4 порядка, вот в этом я запутался... (((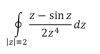
Или полюс 4 порядка, вот в этом я запутался... (((
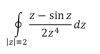
Мне кажется, что это полюс третьего порядка.
Для числителя f(z)=z-sinz точка z=0 - нуль первого порядка, тогда эту функцию можно записать в виде: f(z)=z*f1(z), причем f1(0)<>0.
Тогда подынтегральная функция запишется в виде: z*f1(z)/2z^4=[f1(z)/2]/z^3.
Автор: Руководитель проекта 16.11.2008, 11:26
z=0 - полюс первого порядка.
Автор: tig81 16.11.2008, 11:44
z=0 - полюс первого порядка.
а почему? Где ошибка в моих рассуждениях?
Все, нашла. Я просто не умею брать производную от f(z)=z-sinz.
Тогда исправляюсь: f(z)=z^3*f1(z)
Подынтегральная функция z^3*f1(z)/2z^4=[f1(z)/2]/z. Т.е. z=0 - простой полюс.
Автор: Руководитель проекта 16.11.2008, 12:06
Все, нашла. Я просто не умею брать производную от f(z)=z-sinz.
Не ошибается тот, кто ничего не делает. По себе знаю
Важно уметь признавать их.
Автор: tig81 16.11.2008, 12:12
Не ошибается тот, кто ничего не делает. По себе знаю
Важно уметь признавать их.
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
