Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Геометрия _ окружность, две касательный и точка
Автор: bratic 3.1.2008, 13:00
Вот в чем проблеиа. Как решить ГРАФИЧЕСКИ задачу: построить окружность используя две касательных и точку. ![]()
Автор: tig81 3.1.2008, 14:00
Вот в чем проблеиа. Как решить ГРАФИЧЕСКИ задачу: построить окружность используя две касательных и точку.
а что за точка задана?
Автор: bratic 3.1.2008, 19:35
а что за точка задана?
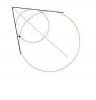
на рисунке показано просто две касательные и отдельно стоящая точка (никак не связана с касательными). То что черным нарисовано то задано, что красноватым то то, что нужно нужно получить
Эскизы прикрепленных изображений
Автор: venja 4.1.2008, 6:58
Ясно, что центр этой окружности лежит на биссектрисе угла, образованного данными касательными. Постройте эту биссектрису. Теперь задача сводится к такой: на луче (это биссектриса) построить точку (это и будет центр искомой окружности), равноудаленную от одной (любой) из касательных и заданной точки. Дальше не думал.
Можно другую идею попробовать.
Вписать в угол двух касательных ЛЮБУЮ окружность и соединить вершину угла А с заданной в задаче точкой М (через которую должна проходить искомая окружность). Прямая АМ пересечет построенную окружность в некоторой точке С.
Тогда, думаю (попробуйте доказать это или нечто аналогичное), что отношение АМ:АС равно отношению расстояний от А до центров искомой и построенной окружностей.
Автор: bratic 4.1.2008, 14:39
Ясно, что центр этой окружности лежит на биссектрисе угла, образованного данными касательными. Постройте эту биссектрису. Теперь задача сводится к такой: на луче (это биссектриса) построить точку (это и будет центр искомой окружности), равноудаленную от одной (любой) из касательных и заданной точки. Дальше не думал.
Можно другую идею попробовать.
Вписать в угол двух касательных ЛЮБУЮ окружность и соединить вершину угла А с заданной в задаче точкой М (через которую должна проходить искомая окружность). Прямая АМ пересечет построенную окружность в некоторой точке С.
Тогда, думаю (попробуйте доказать это или нечто аналогичное), что отношение АМ:АС равно отношению расстояний от А до центров искомой и построенной окружностей.
Спасяб
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
