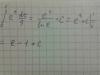Версия для печати темы

Автор: Fiedel 24.5.2015, 11:11

помогите пожалуйста с интегралом
e^(3x^3-1)*x^2dx
делала замену t=3x^3-1, новые границы интеграла -1 и 2, а с x^2 не знаю что делать, там же первоначальные границы
ещё дважды по частям пыталась, но тоже не выходит
u=e^(3x^3-1)
du=9x^2(3x^3-1)
dv=x^2
v=x^3/3
получается e^(3x^3-1)*x^2-int(x^3/3*9x^2(3x^3-1)*e^3x^3-1))
u=e^3x^3-1
dv=27x^5-x^2
v=?

Автор: граф Монте-Кристо 24.5.2015, 12:15

После того, как сделали замену, нужно пересчитать дифференциал. Чему получилось равно dt?

Автор: Fiedel 24.5.2015, 12:22

dt=9x^2

Автор: граф Монте-Кристо 24.5.2015, 15:37

dx забыли.
И какой в итоге получается интеграл?

Автор: Fiedel 24.5.2015, 15:56

e^tdt/9..?

а нет
в этом-то и проблема
там х^2, а не 3х^3-1

думала разбить на два интеграла, тогда все легко
е^tdt и х^2dx
но так нельзя вроде бы.. границы разные ещё у двух интегралов (после замены ведь нужно менять границы..? там от -1 до 2 получается)

Автор: tig81 24.5.2015, 16:17

интегрируйте теперь по t

Автор: Fiedel 24.5.2015, 16:44

так?
и на 9 наверно умножить нужно

Автор: tig81 24.5.2015, 23:09

c самого начала решение покажите, пожалуйста