Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Ряды _ как доказать, что 1/n ряд расходится
Автор: staff 24.6.2012, 7:09
Всем привет, как доказать, что ряд расходится
Эскизы прикрепленных изображений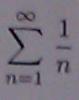
Автор: Dimka 24.6.2012, 7:58
По интегральному признаку можно доказать
Автор: Руководитель проекта 24.6.2012, 11:45
В любом учебнике по мат. анализу есть доказательство.
Автор: staff 24.6.2012, 13:04
В любом учебнике по мат. анализу есть доказательство.
позже приступлю.... Готовлюсь к эзкамену компьютерной сети, оказалось там по хуже дела.... Подробнее тут
http://www.prepody.ru/topic14940.html ну и чуть ниже в ветке о себе
Автор: staff 24.6.2012, 16:29
Думаю это ничего не доказывает.....
http://img.prado.lt/?v=2012062419.jpg
Автор: граф Монте-Кристо 24.6.2012, 23:53
1/1 + 1/2 + (1/3 + 1/4) + (1/5 + 1/6 + 1/7 + 1/8) +... > 1 + 1/2 + (1/4 + 1/4) + (1/8 + 1/8 + 1/8 + 1/8) + ... = 1 + 1/2 + 1/2 + 1/2 + ...
Получаем, что сумма гармонического ряда больше суммы ряда 1 + 1/2 + 1/2 + 1/2 + ..., который, очевидно, расходится. Следовательно, гармонический ряд тоже расходится.
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
