Здравствуйте!

Подскажите пожалуйста решение примера.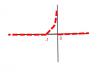




получается по данной системе график правильно построен?
нужно найти параметр "а" при которой эта функция будет плотностью вероятности случайных величин

нашел параметр через интеграл, получилось а=5/2

Нужно найти аналитическое представление функции
F(x) = 0 при х<-1 ; 0 при х>0 ; и?

затрудняюсь в последнем уравнеии системы

F(x)=1 при x>0.
Для получения выражения F(x) при -1<x<0 надо найти значение определенного интеграла от (-1) до х от f(x).

получилось при нахождении интеграла: Интеграл (-1 до 0) (5/2)*(х+1)^(3/2)=1


тогда будет последнее уравнение системы 1 при -1<x<0

Почему до 0???



Лучше посмотрите подобный пример. В любом учебнике по теории вероятностей.

извините, не внимателен

(x+1)^(5/2) при -1<x<0

Математическое ожидание тогда находим М(х)=(a+B )/2 (a=-1, b=0) = -1+0/2 = -1/2
так?

Нет, не так. У Вас что - равномерное распределение на (-1,0)?

Общая формула

M(X)=интеграл (от -бесконечность до + бесконечность) x*f(x) dx.

В данном случае

M(X)=интеграл (от -1 до 0) x*f(x) dx.

Для вычисления этого интеграла сделайте замену переменной: x=t-1

да, я понял, у нас же не прямая.

Дисперсию находим как D(x)=M(x^2)-(M(x))^2 либо Интеграл (-00 до +00) ((x-M(x))^2) *f(x) dx

Спасибо за помощь! все решил!