Здравствуйте, гость ( Вход | Регистрация )
  |
| Cann88 |
 28.11.2009, 20:44 28.11.2009, 20:44
Сообщение
#1
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 28.11.2009 Город: Томск Вы: студент |
Как в среде MathCAD записать характеристическое уравнение и решить его? (IMG:style_emoticons/default/sad.gif)
|
| tig81 |
 28.11.2009, 20:53 28.11.2009, 20:53
Сообщение
#2
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Характеристическое уравнение чего?
Maple не подойдет? |
| Cann88 |
 29.11.2009, 4:52 29.11.2009, 4:52
Сообщение
#3
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 28.11.2009 Город: Томск Вы: студент |
Характеристическое уравнение чего? Maple не подойдет? Может и подойдет det([Y]-lambda[E])=0 вот Хар уравнение, где Y моя матрица Это просто же надо определитель, у которого по диагонали стоит коэфф-lambda приравнять к нулю? Только как это сделать? Собственные числа можно найти матрицы, но это же немного не то будет? |
| tig81 |
 29.11.2009, 7:30 29.11.2009, 7:30
Сообщение
#4
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Может и подойдет тогда ловите (IMG:http://i070.radikal.ru/0911/0d/656f528e32d1.jpg) Цитата det([Y]-lambda[E])=0 вот Хар уравнение, где Y моя матрица т.е. характеристическое уравнение матрицы для нахождения собственных значений Цитата Собственные числа можно найти матрицы, но это же немного не то будет? Все зависит от задания П.С. для маткада поищите на exponenta.ru или в гугле. Должно где-то же быть описание. |
| Cann88 |
 29.11.2009, 12:04 29.11.2009, 12:04
Сообщение
#5
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 28.11.2009 Город: Томск Вы: студент |
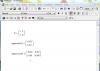 Вот это тоже самое на MathCAD Но это получить не сложно Так то все верно, но при домножении всех элементов матрицы на одно и тоже число собственные значения изменяются на это же число, чего не должно быть при решении характеристического уравнения, как мне сказали )) Я не пойму как считают эти пакеты, они приравнивают к нулю определитель при нахождении собственных чисел? или просто вычисляет собственные значения матрицы, или это одно и тоже (может я не понимаю чего-то?) Нахождение собственных чисел подразумевает приравнивание к нулю определителя? |
| tig81 |
 29.11.2009, 12:11 29.11.2009, 12:11
Сообщение
#6
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Так то все верно, но при домножении всех элементов матрицы на одно и тоже число собственные значения изменяются на это же число, чего не должно быть при решении характеристического уравнения, как мне сказали )) А зачем вам надо домножать на одно и тоже число? Цитата Я не пойму как считают эти пакеты, они приравнивают к нулю определитель при нахождении собственных чисел? или просто вычисляет собственные значения матрицы, или это одно и тоже (может я не понимаю чего-то?) Какая задача перед вами стоит? Цитата Нахождение собственных чисел подразумевает приравнивание к нулю определителя? Хм... ну как к вам сказать. Собственное число l - это корень характеристического многочлена det(A-lE). Для его нахождения решают характеристическое уравнение det(A-lE)=0. Мне, честно говоря, не совсем понятно, что вам не понятно. Поэтому еще раз повторюсь: какую задачу вы решаете. Четко сформулируйте условие. |
| Cann88 |
 29.11.2009, 15:28 29.11.2009, 15:28
Сообщение
#7
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 28.11.2009 Город: Томск Вы: студент |
А зачем вам надо домножать на одно и тоже число? Какая задача перед вами стоит? Хм... ну как к вам сказать. Собственное число l - это корень характеристического многочлена det(A-lE). Для его нахождения решают характеристическое уравнение det(A-lE)=0. Мне, честно говоря, не совсем понятно, что вам не понятно. Поэтому еще раз повторюсь: какую задачу вы решаете. Четко сформулируйте условие. Есть физическая задачка, где записывается система n вариационных уравнений, вот эти уравнения записываются в матрицу где l это параметр движения у меня,и отрицательность корней l будет являться условием устойчивости, но это не суть важно система имеет нетривиальное решение если выполняется хар уравнение: det(A-lE)=0 Вот задача нахождения l известна как проблема собств. значений. А домножая все элементы матрицы на одно и тоже число(не всегда на одно и тоже конечно-по -разному варьирую) я проверяю как корни ведут себя, но мой руководитель сказал что собственные значения не должны меняться , но я уверен что должны,а вот собственные вектора не меняются ! Вот и я проверяю все варианты , правильно ли я делал до этого и считал |
| tig81 |
 29.11.2009, 20:16 29.11.2009, 20:16
Сообщение
#8
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
я проверяю как корни ведут себя, но мой руководитель сказал что собственные значения не должны меняться , но я уверен что должны,а вот собственные вектора не меняются ! Хм... Если я правильно поняла вас, то вот такое получается (IMG:http://i069.radikal.ru/0911/1b/4c7abdb608e1.jpg) Или не то? |
| Cann88 |
 30.11.2009, 4:06 30.11.2009, 4:06
Сообщение
#9
|
|
Новичок  Группа: Продвинутые Сообщений: 5 Регистрация: 28.11.2009 Город: Томск Вы: студент |
|
| tig81 |
 30.11.2009, 7:48 30.11.2009, 7:48
Сообщение
#10
|
|
Академик         Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Да имеенно это и получается, а собственные вектора не меняются хм... (IMG:http://s39.radikal.ru/i086/0911/dc/c9f6d58e8822.jpg) Я не вижу, чтобы собственные векторы были бы компланарными. В общем я что-то не понимаю и уже начинаю того. (IMG:style_emoticons/default/sad.gif) Надо почитать мат. часть. Цитата Просто я думал что собственные числа тоже не должны меняться при решении хар. уравнения (IMG:style_emoticons/default/unsure.gif) Цитата Спасибо за помощь! Да не за что. |
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 2.8.2025, 16:59 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru









