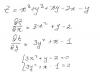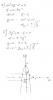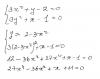Здравствуйте, гость ( Вход | Регистрация )
| OreX |
 29.4.2009, 21:39 29.4.2009, 21:39
Сообщение
#1
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 26.12.2008 Город: Санкт-Петербург Учебное заведение: СПБГИПСР Вы: студент |
|
  |
Ответов(1 - 4)
| Dimka |
 30.4.2009, 3:50 30.4.2009, 3:50
Сообщение
#2
|
|
Доцент       Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
Графически найдите. Постройте графики двух уравнений, точки пересечения - решение уравнения.
|
| OreX |
 30.4.2009, 10:46 30.4.2009, 10:46
Сообщение
#3
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 26.12.2008 Город: Санкт-Петербург Учебное заведение: СПБГИПСР Вы: студент |
|
| Dimka |
 30.4.2009, 11:38 30.4.2009, 11:38
Сообщение
#4
|
|
Доцент       Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
При построении графиков видно, что они имеют четыре точки пересечения, но невозможно установить координаты этих точек. Если решать аналитически, то я пришёл к многочлену четвёртой степени, может быть есть способы нахождения корней этого уравнения с которыми я ещё не знаком?? http://ru.wikipedia.org/wiki/%D0%A3%D1%80%...%B5%D0%BD%D0%B8 |
| OreX |
 1.5.2009, 3:32 1.5.2009, 3:32
Сообщение
#5
|
|
Школьник  Группа: Продвинутые Сообщений: 10 Регистрация: 26.12.2008 Город: Санкт-Петербург Учебное заведение: СПБГИПСР Вы: студент |
Да, видимо здесь бы подошло решение Декарта — Эйлера, но думаю, что будет достаточно просто указать, что критических точек четыре и их диапазон координат.)) Спасибо за помощь.
|
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 3.8.2025, 22:20 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru