Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Дифференцирование (производные) _ Помогите найти критические точки функции двух переменных
Автор: OreX 29.4.2009, 21:39
Дана функция двух переменных, я нашёл частные производные, приравнял их к нулю и теперь не могу найти решение уравнений. Может быть я что-то сделал не так?? Какие есть мысли подскожите плиз!!!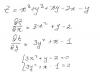
Автор: Dimka 30.4.2009, 3:50
Графически найдите. Постройте графики двух уравнений, точки пересечения - решение уравнения.
Автор: OreX 30.4.2009, 10:46
При построении графиков видно, что они имеют четыре точки пересечения, но невозможно установить координаты этих точек. 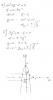
Если решать аналитически, то я пришёл к многочлену четвёртой степени, может быть есть способы нахождения корней этого уравнения с которыми я ещё не знаком??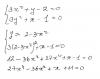
Автор: Dimka 30.4.2009, 11:38
При построении графиков видно, что они имеют четыре точки пересечения, но невозможно установить координаты этих точек.
Если решать аналитически, то я пришёл к многочлену четвёртой степени, может быть есть способы нахождения корней этого уравнения с которыми я ещё не знаком??
http://ru.wikipedia.org/wiki/%D0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5_%D1%87%D0%B5%D1%82%D0%B2%D1%91%D1%80%D1%82%D0%BE%D0%B9_%D1%81%D1%82%D0%B5%D0%BF%D0%B5%D0%BD%D0%B8
Автор: OreX 1.5.2009, 3:32
Да, видимо здесь бы подошло решение Декарта — Эйлера, но думаю, что будет достаточно просто указать, что критических точек четыре и их диапазон координат.)) Спасибо за помощь.
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
