 Вычислить интеграл, используя основную теорему о вычетах |
Здравствуйте, гость ( Вход | Регистрация )
| RaiN17 |
 16.11.2008, 10:21
Сообщение
#1
|
|
Школьник  Группа: Продвинутые Сообщений: 26 Регистрация: 24.5.2008 Город: Сахалинск Вы: школьник  |
Вычислить интеграл, используя основную теорему о вычетах...
Если я все правильно понял то тут единственная особая точка z=0 и это полюс первого порядка. Поправьте меня если я ошибаюсь. Или полюс 4 порядка, вот в этом я запутался... (((  |
   |
 
|
  |
Ответов(1 - 5)
| tig81 |
16.11.2008, 10:46
Сообщение
#2
|
|
Академик Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Цитата(RaiN17 @ 16.11.2008, 12:21)  Если я все правильно понял то тут единственная особая точка z=0 так Цитата и это полюс первого порядка. Поправьте меня если я ошибаюсь. Или полюс 4 порядка, вот в этом я запутался... ((( 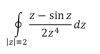Мне кажется, что это полюс третьего порядка. Для числителя f(z)=z-sinz точка z=0 - нуль первого порядка, тогда эту функцию можно записать в виде: f(z)=z*f1(z), причем f1(0)<>0. Тогда подынтегральная функция запишется в виде: z*f1(z)/2z^4=[f1(z)/2]/z^3. |
|
|
|
| Руководитель проекта |
16.11.2008, 11:26
Сообщение
#3
|
|
Руководитель проекта Группа: Руководители Сообщений: 3 189 Регистрация: 23.2.2007 Из: Казань Город: Казань Учебное заведение: КГУ Вы: другое |
z=0 - полюс первого порядка.
|
|
|
|
| tig81 |
16.11.2008, 11:44
Сообщение
#4
|
|
Академик Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Цитата(Руководитель проекта @ 16.11.2008, 13:26) z=0 - полюс первого порядка. а почему? Где ошибка в моих рассуждениях? Все, нашла. Я просто не умею брать производную от f(z)=z-sinz. (IMG:style_emoticons/default/sad.gif) Тогда исправляюсь: f(z)=z^3*f1(z) Подынтегральная функция z^3*f1(z)/2z^4=[f1(z)/2]/z. Т.е. z=0 - простой полюс. |
|
|
|
| Руководитель проекта |
16.11.2008, 12:06
Сообщение
#5
|
|
Руководитель проекта Группа: Руководители Сообщений: 3 189 Регистрация: 23.2.2007 Из: Казань Город: Казань Учебное заведение: КГУ Вы: другое |
Цитата(tig81 @ 16.11.2008, 14:44) Все, нашла. Я просто не умею брать производную от f(z)=z-sinz. (IMG:style_emoticons/default/sad.gif) Не ошибается тот, кто ничего не делает. По себе знаю (IMG:style_emoticons/default/smile.gif) Важно уметь признавать их. |
|
|
|
| tig81 |
16.11.2008, 12:12
Сообщение
#6
|
|
Академик Группа: Преподаватели Сообщений: 15 617 Регистрация: 15.12.2007 Город: Украина, Запорожье Учебное заведение: ЗНУ Вы: преподаватель |
Цитата(Руководитель проекта @ 16.11.2008, 14:06) Не ошибается тот, кто ничего не делает. По себе знаю (IMG:style_emoticons/default/smile.gif) Важно уметь признавать их. (IMG:style_emoticons/default/blush.gif) (IMG:style_emoticons/default/smile.gif) |
|
|
|
|
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0
|
Текстовая версия | Сейчас: 25.5.2025, 11:17 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru