Здравствуйте, гость ( Вход | Регистрация )
| Лера.Н. |
 13.5.2010, 14:19 13.5.2010, 14:19
Сообщение
#1
|
|
Новичок  Группа: Продвинутые Сообщений: 4 Регистрация: 13.5.2010 Город: Воронеж Учебное заведение: ВГТУ Вы: студент |
Доброго времени суток. Очень нужна помощь! Расчет простой электрической цепи.
Начальные данные: R=700 Ом C=800 пФ Е=20е^j28 В f=40 кГЦ Считала и вручную, и с помощью Mathcad. так или иначе получается ток I=7.496*10^-3+j7.694*10^-3; i(t)=0.011cos(wt+46) эквивалентное сопротивление Uэ=12.573+j3.694; uэ(t)=13.1cos(wt+16.38) и Ur=5,247+j5.386; ur(t)=7.519cos(wt+46) Эквивалентное сопротивление считала по правилам последовательного и параллельного соединения сопротивлений. Вопрос у меня такой: может ли в принципе быть такое маленькое значение амплитуды тока? И если нет, подскажите, пожалуйста, где я могла ошибиться. И вопрос про построение векторной диаграммы: что дают в сумме векторы Uэ и Ur, и должна ли эта величина равняться по амплитуде и по фазе данному Е? (простите за, возможно, глупый вопрос) Заранее огромное спасибо! Эскизы прикрепленных изображений 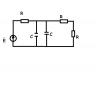
|
  |
Ответов(1 - 6)
| Dimka |
 13.5.2010, 15:08 13.5.2010, 15:08
Сообщение
#2
|
|
Доцент       Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
Доброго времени суток. Очень нужна помощь! Расчет простой электрической цепи. Начальные данные: R=700 Ом C=800 пФ Е=20е^j28 В f=40 кГЦ Считала и вручную, и с помощью Mathcad. так или иначе получается ток I=7.496*10^-3+j7.694*10^-3; i(t)=0.011cos(wt+46) эквивалентное сопротивление Uэ=12.573+j3.694; uэ(t)=13.1cos(wt+16.38) и Ur=5,247+j5.386; ur(t)=7.519cos(wt+46) У меня другие значения получаются. Выкладывайте свое решение, посмотрю. Е=20е^j28 В (28 - это градусы?) |
| Лера.Н. |
 13.5.2010, 17:00 13.5.2010, 17:00
Сообщение
#3
|
|
Новичок  Группа: Продвинутые Сообщений: 4 Регистрация: 13.5.2010 Город: Воронеж Учебное заведение: ВГТУ Вы: студент |
Е=20е^j28 В
28 – да, в градусах. Все остальные фазы тоже в градусах. Zc=1/jwC=-j4.974*10^3 Z(3.4)=Z3+Z4=2R=1.4*10^3 Z(2.3.4)=(Z2*Z(3.4))/(Z2+Z(3.4))=(1.4*10^3*(4.974)j)/(1.4*10^3-4.974*10^3j)=1.297*10^3-j365.149 Zэ=(Z1*Z(2.3.4))/(Z1+Z(2.3.4))=1.063*10^3-j598.481 I=E/(R+Zэ)=20e^j28/(700+(1.063*10^3-j598.481))?=(17.658+j9.4)/(700+(1.063*10^3-j598.481))=(17.658+j9.4)/(1763-j598.481)=(17.658+j9.4)(1763+ j598.481)/(1763^2+598.481^2)= 7.496*10^-3+j7.694*10^-3 Imax=(Im(I)^2+Re(I)^2)^0.5=0.011 фi=arctg(Im(I)/Re(I))=arctg1.027=46 I=0.011*e^j46 i(t)=0.011cos(wt+46) Uz=Zэ*I=(1.063*10^3-j598.481)*( 7.496*10^-3+j7.694*10^-3)=12.573+j3.694 Uzmax=(Im(Uz)^2+Re(Uz)^2)^0.5=13.105 фuz=arctg(Im(Uz)/Re(Uz))=arctg0.294=16.38 Uz=13.1*e^j16.38 uz(t)=13.1cos(wt+16.38) Ur=R*I=700*(7.496*10^-3+j7.694*10^-3)=5.247+j5.386 Urmax= Im(Ur)^2+Re(Ur)^2)^0.5=7.519 фur=фi Ur=7.519*e^j46 ur(t)=7.519cos(wt+46) вот так выглядит моё решение, прошу прощение за формат написанного, нет возможности в более читабельную форму привести. Эскизы прикрепленных изображений 
|
| Dimka |
 13.5.2010, 19:06 13.5.2010, 19:06
Сообщение
#4
|
|
Доцент       Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
Верно. У меня просто некоторые отличия в цифрах после запятой.
Для построения векторной диаграммы напряжений постройте вектор Ur и Uz. Сложите их геометрически (по правилу параллелограмма). После сложения должен получиться вектор E длинной 20 и углом наклона 28град. |
| Лера.Н. |
 14.5.2010, 8:00 14.5.2010, 8:00
Сообщение
#5
|
|
Новичок  Группа: Продвинутые Сообщений: 4 Регистрация: 13.5.2010 Город: Воронеж Учебное заведение: ВГТУ Вы: студент |
огромное спасибо!
меня просто смутила слишком маленькая амплитуда тока, по сравнению с амплитудой напряжений, те так и должно быть, да? |
| Dimka |
 14.5.2010, 9:29 14.5.2010, 9:29
Сообщение
#6
|
|
Доцент       Группа: Преподаватели Сообщений: 4 925 Регистрация: 26.2.2007 Город: _ Вы: другое |
да
|
| Лера.Н. |
 14.5.2010, 9:44 14.5.2010, 9:44
Сообщение
#7
|
|
Новичок  Группа: Продвинутые Сообщений: 4 Регистрация: 13.5.2010 Город: Воронеж Учебное заведение: ВГТУ Вы: студент |
еще раз огромное спасибо!!!
|
  |
1 чел. читают эту тему (гостей: 1, скрытых пользователей: 0)
Пользователей: 0

|
Текстовая версия | Сейчас: 4.8.2025, 6:52 |
Книжки в помощь: "Сборник заданий по высшей математике" Кузнецов Л.А., "Сборник заданий по высшей математике" Чудесенко В.Ф., "Индивидуальные задания по высшей математике" Рябушко А.П., и другие.
Русская версия Invision Power Board
v2.1.7 © 2025 IPS, Inc.
Зеркало сайта Решебник.Ру - reshebnik.org.ru









