Версия для печати темы

Автор: Danilka 20.2.2010, 14:43

помогите пожалуйста с уравнениями:

1) y''+y=ctgx

(это линейное неоднородное дифференциальное уравнение нужно решать вроде бы методом вариации произв. постоянных)

2) y''''- 8*y' = (x^2) + 1 + x*sin((3^(1/2))*x) - 2*e^(2*x)

обозначения(на всякий случай) : '''' - четыре штрих
* - обычное умножение
^ - возведение в степень

(решать нужно вроде бы методом подбора частных решений)



спасибо большое)

Автор: граф Монте-Кристо 20.2.2010, 14:50

1)Можно решать по-разному,но лучше,действительно,вариацией постоянных.
2)Сначала решаете однородное,потом ищете частное решение неоднородного для каждого слагаемого.

Автор: Danilka 20.2.2010, 14:54

первое более менее получается решать, но ответ неправильный получается всегда(

второе вообще не представляю как делать, не знаю этих способов решения я ((

Автор: Danilka 20.2.2010, 17:15

первое решил

проверьте ответ пожалуйста




Эскизы прикрепленных изображений

Автор: Dimka 21.2.2010, 8:33

верно

Автор: Danilka 21.2.2010, 14:44

спасибо, хорошо, что верно)

а вот второй как решать непредставляю..не имел дел с порядком выше второго пока что

может кините ссылку на решение подобного примера, пожалуйста ? только не на учебную литературу пожалуйста , я в ней путаюсь , тем более она у меня есть , только без образцов решений (

Автор: Dimka 21.2.2010, 15:44

составляйте характеристическое уравнение однородного диф.уравнения, ищите его корни. Сколько получилось?

Автор: Dimka 21.2.2010, 16:25

Г.И. Запорожец "Руководство к решению задач по математическому анализу" стр. 404 и далее

Автор: Danilka 21.2.2010, 20:40

у0 =



у1 = посчитал



у2 = НЕ МОГУ НИКАК ПРОДИФФЕРЕНЦИИРОВАТЬ ЧЕТЫРЕ РАЗА




у3 = 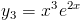НЕ МОГУ НИКАК ПРОДИФФЕРЕНЦИИРОВАТЬ ЧЕТЫРЕ РАЗА



при нахождении у2 и у3 у меня получаются огромнейшие числа, не получается у меня никак их посчитать

Автор: Dimka 21.2.2010, 20:53

y0 - неверно нашли. Запишите характеристическое уравнение.Какие корни характеристического уравнения получились?

Автор: Danilka 22.2.2010, 9:33

(лямбда^4)-(8*лямбда)=0

лямбда1 = 0
лямбда = 2

вот так я начал решать

Автор: Dimka 23.2.2010, 10:04

комплексные корни потеряли

(лямбда^4)-(8*лямбда) нужно разложить на множители

Автор: Danilka 23.2.2010, 13:12

ну :

(лямбда)*(((лямбда^3)-8) = 0

лямбда1 = 0
лямбда2 = 2

Автор: Dimka 23.2.2010, 13:21

(p^3)-8 дальше раскладывайте как разностьт кубов

p.s. вместо лямбда используем p

Автор: Danilka 23.2.2010, 17:32

p*(p-1)*((p^2)+p+1) = 0

Автор: Dimka 23.2.2010, 18:10

разложение не верно.
p*(p-1)*((p^2)+p+1)=p^4-p, а у Вас p^4-8p

Автор: Danilka 23.2.2010, 19:53

тьфу блин..простите.. вообще не туда взглянул

p*(p-8)*((p^2)+8p+64)

Автор: Dimka 23.2.2010, 19:58

p*(p-8)*((p^2)+8p+64)=p^4-512*p

Автор: Danilka 24.2.2010, 14:26

p*(p-2)*((p^2)+2p+4)

Автор: Dimka 24.2.2010, 14:54

Ну вот, теперь ищите кони, приравняв каждый из сомножителей к 0
p=0, p1=0,
p-2=0, p2=2,
((p^2)+2p+4)=0, p3=..., p4=....

сколько p3 и p4 получилось?