Версия для печати темы

Автор: clink 7.1.2010, 14:58

решаю такую задачку:

Случайная величина Х задана дифференциальной функцией распределения. Требуется найти параметр а, интегральную функцию, математическое ожидание, дисперсию, среднеквадратическое отклонение, построить графики интегральной и дифференциальной функций, найти вероятность попадания случайной величины Х в интервал (α, β):

f(x):=
0, if |x| >1,

[a / (1+x^2) ], if |x| <=1.

α:=0, β:= 1/sqrt(3)

Я, читая методичку пришел к выводу, что случайная величина у меня задана не "дифференциальной функцией", а плотностью распределения, потому что ведь требуется еще и найти "интегральную функцию", а это тоже самое, что и дифференциальная функция. (Поправьте, если не прав, но, зная печальный опыт общения с нашим институтом, вполне допускаю наличие ошибок в задании. такое бывает неоднократно)


Поэтому решаю по предложенному в методичке алгоритму:

чтобы найти параметр а, пользуюсь свойством, что интеграл от функции плотности будет равен единице, т.е.

a * int(dx/1+x^2) = pi/4 * a. (а сразу вынес, пределы взял от 0 до 1, т.к. |x|<=1) - не уверен насчет пределов. решал дальше: pi/4 *a = 1, => a = 4/pi.

потом нахожу интегральную функцию по свойству F(x)= indef. int [ f(x)dx ]

1) f(x):=0, if |x|>1 => F(x):= indef.int(0dx) = 0.

2) f(x):=a/(1+x^2), if |x|<=1, => F(x):a*int [dx / (1+x^2)] (от -1 до x, a:=4/pi) все это получилось равно 4/pi * arctg(x^2) - 1.

Очень хочется проверить себя на ошибки на данном этапе заранее благодарен!

Автор: malkolm 7.1.2010, 16:48

Физики обычно плотность распределения называют дифференциальной функцией распределения, а функцию распределения - интегральной функцией распределения. С точки зрения этой физической терминологии всё в условии верно.

Функция распределения не является неопределённым интегралом от плотности распределения. F(x) - это интеграл в границах от -оо до х от f(t)dt. Функция, которая у Вас получилась, не может быть функцией распределения, т.к. не обладает ни одним из трёх обязательных свойств функций распределения.

Автор: Juliya 7.1.2010, 21:39

и а неверно найдено.. а=2/пи (где ж в какой школе Вас модулям учили -

Автор: clink 8.1.2010, 19:26

спасибо за указание на мои ошибки, пределы попутал из-за спешки.

но теперь я не понимаю какую дифференциальную функцию мне взять для интегрирования, чтобы получить значение интегральной функции для +00, получается, что точно не нуль, ведь надо чтобы была единица.... остается только 1/(1+x^2), но ведь это функция распределения для интервала от -1 до 1...а область +00 это x>1.. а там еще и модуль - получается что для -00, что для +00 одно значение функции будет.... че-то совсем запутался

Автор: Juliya 8.1.2010, 21:55

Функция распределения - это всегда интеграл от -оо до х, для любого текущего х. Т.к. функция плотности f(x) имеет три участка, такие же три участка должна иметь с разными значениями и функция распределения. Вот и интегрируйте её в названных пределах, когда х расположен на всех трех участках...
где-то недавно была такая темка.. поищите...

Автор: Juliya 9.1.2010, 0:26

например:
http://www.prepody.ru/topic8594.html?hl=%F4%F3%ED%EA%F6%E8%FF+%F0%E0%F1%EF%F0%E5%E4%E5%EB%E5%ED%E8%FF

http://www.prepody.ru/topic7305.html?hl=%F4%F3%ED%EA%F6%E8%FF+%F0%E0%F1%EF%F0%E5%E4%E5%EB%E5%ED%E8%FF

ту, что искала, не нашла...

Автор: clink 9.1.2010, 7:13

Спасибо!! Я вроде понял!
эти модули с толку сбили. получается так:

1) f(x):=0, -oo < x < -1 *** F(x):= int(-oo, 0){0dx}=0

2) f(x):=a / (1+x^2), -1<=x<=1 *** F(x):=int(-1,1) (2/pi)*{dx/(1+x^2)}=1

3) f(x):0, 1 <x < +oo *** F(x):= 1 + int(1,+oo) {0dx} = 1.

теперь удовлетворяет свойствам функции распределения, правильно?

Эх, завтра экзамен, осталось две задачки дорешать в контрольной...



посчитал математическое ожидание, скажите пожалуйста, правильно ли?



тогда получается и дисперсия равна нулю?

Автор: Juliya 9.1.2010, 10:06

Цитата(clink @ 9.1.2010, 10:13)

Цитата(clink @ 9.1.2010, 10:13)

Автор: clink 9.1.2010, 11:06

F(x):=

if x<-1, int(-oo,x){0dx} = 0

if |x|<1, int(-oo,x){f(x)dx} = int(-oo,-1){0dx} + int(-1,x) (2/pi)*{dx/(1+x^2)} = 0 + (2/pi)*[arctg(x)| from -1 to x] = [2arctg(x)/pi] +1

if x>1, int(-oo,-1){0dx} + int(-1,1) (2/pi)*{dx/(1+x^2)} + int(1,+oo){0dx} = 1.

так?

а дисперсию получается только на участке -1;1 считаем, раз в остальных функция постоянна?

D(X):= int(-1,1) { (x-M(X))^2*f(x)dx} = int(-1,1) (2/pi)*{ x^2dx/(1+x^2)} = (2/pi)*(2-pi/2)=(4/pi)-1 = 0.273

проверьте пожалуйста?

Автор: Juliya 9.1.2010, 11:18

вольфрам понра?

ну теперь почти... только проверьте вручную - там такая константа получается?

http://www.wolframalpha.com/input/?i=int+%282%2F%28pi*%281%2Bx^2%29%29%29dx+-1+to+x

Автор: clink 9.1.2010, 11:40

ага, понравился
че-то не пойму я почему вольфрам там одну четвертую насчитывает там же получается arctg(x) - arctg(-1) = arctg(x)- (-pi/2) =arctg(x)+pi/2. а потом все это умножается на параметр а=2/pi, дробь сокращается, остается 2*arctg(x)/pi...
правда я и сам вижу, что что-то не так, так как график в маткаде на это участке зашкаливает за -1 и 1, а ведь этого быть не может

тьфу... пи же это 180.. заклинило у меня 90... теперь я понимаю зачем продавцы в магазине, когда им даешь полтинник, а покупаешь единственный товар за 40 рублей, отнимают на калькуляторе 50 - 40...

тогда конечно (2/pi)*(arctg(x)+pi/4) получается, и функция на этом участке выглядит как (2arctg(x)/pi)+1/2


красота: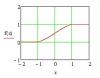


а можь рано радуюсь... Juliya, скажите пожалуйста, правильно?

Автор: Juliya 9.1.2010, 12:13

Цитата(clink @ 9.1.2010, 14:40)

ага, понравился
че-то не пойму я почему вольфрам там одну четвертую насчитывает там же получается arctg(x) - arctg(-1) = arctg(x)- (-pi/2) =arctg(x)+pi/2. а потом все это умножается на параметр а=2/pi, дробь сокращается, остается 2*arctg(x)/pi...
правда я и сам вижу, что что-то не так, так как график в маткаде на это участке зашкаливает за -1 и 1, а ведь этого быть не может

тьфу... пи же это 180.. заклинило у меня 90... теперь я понимаю зачем продавцы в магазине, когда им даешь полтинник, а покупаешь единственный товар за 40 рублей, отнимают на калькуляторе 50 - 40...

тогда конечно (2/pi)*(arctg(x)+pi/4) получается, и функция на этом участке выглядит как (2arctg(x)/pi)+1/2
красота:


а можь рано радуюсь... Juliya, скажите пожалуйста, правильно?

Автор: clink 9.1.2010, 12:16

согласен. Просто привык в маткаде так писать.
Спасибо

Автор: Juliya 9.1.2010, 12:31

и дисперсия, т.к. М(Х)=0, равна начальному моменту второго порядка:
http://www.wolframalpha.com/input/?i=int+%282x^2%2F%28pi*%281%2Bx^2%29%29%29dx+-1+to+1

Автор: clink 9.1.2010, 12:33

а дисперсию я выше написал, также посчитал. Щас еще осталось посчитать вероятность попадания в интервал, но с этим я думаю справлюсь

видел в Гмурмане про эти моменты, но не вникал еще... был в шоке, что какой-то там момент геометрически является центром масс.... понял, что теория вероятности - это очень "страшная" штука, которая как и все в математике вылезает к одному и тому же: интегралам, дифференциалам и рядам

Автор: Juliya 11.1.2010, 13:54

да нет, не такая уж и страшная.. а математику в виде интегралов и производных (ряды очень уж редко) она использует только по мере своих нужд...

Вот, например, что такое функция распределения? Вы сразу в интегралы углубились, а надо было сначала её суть понять... а её суть - это ВЕРОЯТНОСТЬ того, что случайная величина в результате испытания примет значения, МЕНЬШЕ какого-то интересующего нас значения х. а потом уже, в зависимости от нашей случайной величины - либо просто суммируем все нужные вероятности для дискретной, либо интегрируем, если имеем непрерывную случайную величину... Тогда бы 0 на +оо Вы точно бы не получили - ведь слева у нас находятся все возможные значения случайной величины, значит, вероятность попасть левее равна 1.

зы. как, кстати, экзамен?