Версия для печати темы

Автор: maxlav 12.12.2009, 9:54

Доброго времени суток.

На квадрат случайно с равномерным распределением бросают частицу. Найти вероятность того, что она удалена от вершин квадрата на расстояние, не меньше половины длины стороны квадрата.

На сколько я понял: частица может попасть в любую область квадрата.
За событие А я принял расстояние от точки до вершины. Если наименьшее растояние - половина длины стороны a/2 (точка находится на ребре), то максимальное расстояние (√5*a)/2.
По геометрическому методу: mes(A)/mes(Ω)=((√5*a)/2 - a/2)/a

Решение забраковано, в чем я ошибся?

Автор: Juliya 12.12.2009, 10:28

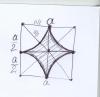
расстояние от любой ВЕРШИНЫ должно быть больше, чем а/2. т.е. надо найти вер-ть попадания вот в такую заштрихованную область:


Эскизы прикрепленных изображений

Автор: Ярослав_ 12.12.2009, 11:34

http://radikal.ru/F/i081.radikal.ru/0912/77/e9b8a9893997.jpg

Автор: Juliya 12.12.2009, 11:50

Спасибо! я по-быстрому, по-старинке.. это в Вольфраме? Я уже даже скачала, но разобралась только с расчетами и функциями.. Как жаль, что раньше не было у меня такой программки.. сколько времени я потратила на расчет всяких интегралов и т.п. при составлении ответов ...
а где и как там графики строят?

ps сорри за OFF

Автор: Ярослав_ 12.12.2009, 14:50

В верхней панельке Help->Documentation Center->Function Visualization
там уже заготовки имеются, только нужно свои данные забивать, ну и остальное по-надобности, вроде линий широких, разного (одинакового) цвета и т.д.

Такой квадратик как этот, можно построить с помощью функций, наверняка есть и другой способ, только я ещё не знаю... Именно для данной картинки, где а=1

RegionPlot[{x^2 + y^2 < 1/4, x^2 + (y - 1)^2 < 1/4, (x - 1)^2 + y^2 < 1/4, (x - 1)^2 + (y - 1)^2 <1/4},{x, 0, 1}, {y, 0, 1},PlotStyle -> Pink, Background -> LightBlue]

За примерами я хожу http://www.exponenta.ru/educat/class/courses/student/courses.asp.

Автор: Juliya 12.12.2009, 15:01

Спасибо!

мы тут стараемся, а автор и не появляется...

кстати, хотела спросить, откуда он вообще √5 взял??

Автор: maxlav 14.12.2009, 18:41

Автор здесь - просто в интернете не живу.
Julia, спасибо за помощь, взглянул на риснок - понял в чем был не прав.
А √5a - диагональ располовиненного квадрата, в смысле прямоугольника со сторонами a и a/2.
Еще раз спасибо!

OFF:
Ярослав_, а можно по-подробней про чудесное ПО (Вольфрам).