Версия для печати темы

Автор: MoDeJIueR 7.11.2009, 7:52

Помогите пожалуйста найти производную данной функции...
Заранее премного благодарен


Эскизы прикрепленных изображений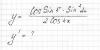

Автор: Dimka 7.11.2009, 7:59

Что не получается?

Автор: MoDeJIueR 7.11.2009, 8:10

Вот 2 раза пробовал взять производную самостоятельно, истины не достиг...
Не знаю даже как сформулировать, что конкретно у меня не получается.



Эскизы прикрепленных изображений

Автор: Dimka 7.11.2009, 8:13

Вы логарифмическое дифференцирование проходили?

Автор: MoDeJIueR 7.11.2009, 8:15

Мне этот термин к сожалению ни о чем не говорит(
Это типовой расчет и его можно решать любыми доступными способами...
Присутствовал на всех лекциях, но лог.дифференцирования не помню...

Автор: Dimka 7.11.2009, 8:20

y=((cos sin5)/2 )*[(sin2x)^2 / cos4x]

то, что в круглых скобках - константа, ее не трогают и выносят за знак производной. Теперь нужно найти производную выражения в квадратных скобках. Можете найти?

Автор: Julia 7.11.2009, 8:27

Можно сначала сделать замену (sin 2x)^2 = (1 - cos 4x)/2. Тогда вычисление производной упростится.

Автор: MoDeJIueR 7.11.2009, 8:29

Вот, проверьте пожалуйста правильно ли я сделал.

Автор: Julia 7.11.2009, 8:33

Неверно, сделайте сначала замену

((sin 2x)^2)'= 4 sin 2x* cos 2x

Автор: Dimka 7.11.2009, 8:33

Нет, производная от (sin2x)^2=2*sin(2x)*cos(2x)*2=2sin(4x)

Автор: MoDeJIueR 7.11.2009, 8:38

Если решать через замену, то я правильно делаю ? или опять косячу ?(

Автор: Julia 7.11.2009, 8:42

(1/cos(4x))' = ((cos(4x))^(-1))' = -1*(cos(4x))^(-2)*(cos(4x)')=-1*(cos(4x))^(-2)*(-sin(4x))*(4x)'=(4sin(4x)/(cos(4x))^2)

Автор: MoDeJIueR 7.11.2009, 8:51

Вот проверьте пожалуйста.

Автор: Julia 7.11.2009, 8:56

Теперь верно

Автор: MoDeJIueR 7.11.2009, 9:10

Огромное спасибо за вашу помощь