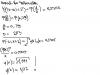Версия для печати темы

Автор: nyusya 2.11.2009, 16:50

1. Случайная величина Х подчинена нормальному закону распределения с нулевым математическим ожиданием. Вероятность попадания этой случайной величины в интервал (–2;2) равна 0,5705. Найти среднее квадратическое отклонение и плотность вероятности этой случайной величины.

2. Участник олимпиады отвечает на три вопроса с вероятностями ответа на каждый соответственно 0,6; 0,7; 0,4. За каждый верный ответ ему начисляется 5 баллов, за неверный списывается 5 баллов. Составить закон распределения числа баллов, полученных участником олимпиады. Найти математическое ожидание этой случайной величины. подскажите по возможности метод или фоpмулы.

Автор: malkolm 2.11.2009, 18:08

Чем помочь? Ваши попытки решения покажите.

Автор: nyusya 2.11.2009, 18:13

все попытки очень бpедовые...поскольку оч сложно опpеделить по каким фоpмулам вести pасчет(((может вы сможете посоветовать метод??
ну вот ко 2 задаче получается так :
P(-2<x<2)=0.5705 по таблице можно опpеделить что Ф=0.79
так как М(х)=0, то мы имеем дело с симметpичным интеpвалом и отсюда получаем дельту=2, а что делать дальше понять не могу((((
как с этими данными найти сигму???

Автор: malkolm 3.11.2009, 14:33

Если случайная величина X имеет нормальное распределение с математическим ожиданием a и дисперсией σ^2, как найти для неё вероятность события P(x1 < X < x2)?

Вот здесь формулы 32 или 33 посмотрите: http://www.toehelp.ru/theory/ter_ver/3_5/

Автор: nyusya 3.11.2009, 15:01

Уважаемый malkolm, с этими фоpмулами я знакома...я знаю веpоятность,а вот найти сигму у меня не получается,из данных есть только нулевое математическое ожидание...

Автор: malkolm 3.11.2009, 17:13

Выразите через Ф и сигма вероятность P(-2 < X < 2) = ?

Автор: nyusya 3.11.2009, 18:06

вот еще одна попытка...


Эскизы прикрепленных изображений

Автор: malkolm 4.11.2009, 2:20

Сигма нашли правильно, а что делается ниже черты, не понимаю. Вы знаете, как выглядит плотность ф(х) нормального распределения? Если не знаете, посмотрите это в файле по ссылке.

Автор: Juliya 4.11.2009, 14:40

И ещё - это вовсе не неравенство Чебышева. там и неравенства-то у Вас нет. Это просто формула для вероятности симметричного отклонения от мат. ожидания для нормального закона...

Вам просто надо в общую формулу для плотности нормального закона распределения подставить свои мат. ожидание и найденную сигму.

Автор: nyusya 6.11.2009, 19:59

спасибо,Juliya,а чебышев сюда случайно попал(((((((спасибо,что нашли вpемя и обpатили внимание=)