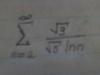Версия для печати темы

Нажмите сюда для просмотра этой темы в обычном формате

Образовательный студенческий форум _ Ряды _ Исследовать ряд на сходимость

Автор: foRmAt 25.5.2007, 12:50

Здравствуйте,помогите пожалуйста исследовать ряд на сходимость,не знаю с чего начать.

Автор: KaLLa4 28.5.2007, 18:56

Точно не знаю, но по моему тут нужно воспользоваться интегральным Признаком Коши.

то есть в конце преобразований предела получится что a/b при условии ,что b>a следовательно предел < 1 , а значит ряд сходится.

Автор: sonka 29.5.2007, 7:49

помогите, пожалуйста исследовать на сходимость ряд от 1 до бескончности: сумм(n^2)*(sin(pi/2n))^n
заранее спасибо smile.gif

Автор: venja 29.5.2007, 8:20

Сравним этот ряд с рядом
(n^2)*(1/sqrt(2))^n
Этот ряд сходится (можно это доказать по признаку Даламбера), а его общий член больше общего члена исходного ряда , так как
sin(pi/2n)<=sin(pi/4). Тогда по теореме сравнения исходный ряд сходится.

Автор: sonka 29.5.2007, 23:51

Спасибо большое. Только я не пойму как связана дробь с корнем из 2^n в знаменателе с синусом пи на четыре. wacko.gif
Жаль, что сама не нашла ряд для сравнения.

P.S.: А!!! Поняла! 1/sqrt(2) - это же синус пи на четыре. Все, спасибо, спасибо, спасибо.smile.gif smile.gif smile.gif

Автор: Lavezza 26.6.2007, 18:18

помогите ,пожалуйста,исследовать ряд на сходимость ряд от 2 до бесконечности: сумм (3^1/2) /(5^1/2lnn) sad.gif

Автор: venja 26.6.2007, 18:37

Расставьте скобки.
Не думаю, что n есть только под логарифмом. Проверье.

Автор: Lavezza 26.6.2007, 18:51

ПОСМОТРИТЕ ТАК))):


Эскизы прикрепленных изображений
Прикрепленное изображение

Автор: Руководитель проекта 27.6.2007, 5:00

Тогда зачем константы под знаком суммы?
Ряд расходится. Можно применить http://reshebnik.ru/solutions/6/3/ и сравнить данный ряд с гармоническим рядом.

Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)