Версия для печати темы

Автор: sanchos92 4.10.2009, 7:45

Уважаемые посетители,модераторы форумы вы не могли бы мне помочь решить вот такое задание: Дана функция:     g( x ) = x^ 2 − 3 x + 2 − | x^2 − 5 x + 4 |+a  найти все значения а при которых она пересекает ось абсцисс менее чем в 3ех различных точка.Мои рассуждения таковы: я рассмотрел функцию на двух различный ромежутках при x<= 1 и x=>4 у меня получилась функция y=2x-2+a которая всегда будет иметь 1 корень т.к k не равно 0 а во втором случае при 1<x <4 получилась функция y=2x^2-8x+6 +a рассматривая дискриминант у этой фукций будет меньше 2ух корней если a<= -2 .Таким образом образом мой ответ a<=-2.Может подсказать в чем моя ошибка.
P.S меня интерсует только аналитичексй ход решения. Спасибо

Автор: tig81 4.10.2009, 7:57

Цитата(sanchos92 @ 4.10.2009, 10:45)

Автор: sanchos92 4.10.2009, 8:35

Это диганостический ЕГЭ,там вот такой график получается при графическом решении , но мне аналитка интересна


Эскизы прикрепленных изображений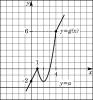

Автор: tig81 4.10.2009, 9:27

Цитата(sanchos92 @ 4.10.2009, 11:35)

Автор: Dimka 4.10.2009, 9:29

при a=(-беск;0]U[2; беск) она пересекает ось абсцисс менее чем в 3ех

Автор: tig81 4.10.2009, 9:44

Автор: sanchos92 4.10.2009, 11:21

хорошо,график это решение графическое

Автор: sanchos92 4.10.2009, 12:17

мое решение
1.Рассмотрим функцию y=x^ 2 − 3 x + 2 − | x^2 − 5 x + 4|+a на промежутке x<=1, x>=4 ,на этом промежутке у нас получитьс функция y=2x-2+a , которая всегда будет пересекаь ось абсцисс в единственной точке
2.Рассмотрим функцию y=x^ 2 − 3 x + 2 − | x^2 − 5 x + 4|+a на промежутке 1<x<4 на этом промужутке у нас получиться функция y=2x^2-8x+6 +a. Найдем количество корней уравнения 2x^2-8x+6 +a=0
D=64-4*2*(6+a)
D=16-8a
при а>=2 график пересекает функцию менее чем 2 раза.Следовательно функция имеет менее 3ех корне при a>=2

Автор: граф Монте-Кристо 4.10.2009, 12:47

Во втором пункте при рассмотрении дискриминанта Вы не учли,что корни могут не попасть в [1;4].

Автор: sanchos92 4.10.2009, 13:31

тогда как я понимаю нужно вот такое условие 1<x<4 т.е 1 <8+-sqrt(16-8a)/4<4 тогда мы найдем те а при которых уравнение будет иметь два корня на данном промежутке

Автор: граф Монте-Кристо 4.10.2009, 13:36

По-моему,с графиком гораздо проще.

Автор: sanchos92 4.10.2009, 13:50

да действительно

Автор: tig81 4.10.2009, 14:07