Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Дифференциальные уравнения _ y'=(7x+2y-1)/(8x-3y+2), y"=y' * lny'/y
Автор: Neolina 3.6.2009, 17:46
1) y'=(7x+2y-1)/(8x-3y+2) Методом Вариации и Бернулли
2) y"=y' * lny'/y С заменой на y'
3) y"+(x-3)y'=0 С заменой на y'
4) (x+15)y"(x)+7y'(x)+8y(x)=14 y(0)=1, y'(0)=2 По методу Маклорена, первые четыре члена.
Пожалуйста помогите....
Автор: Skiper 3.6.2009, 17:53
что именно то не получается?
читайте http://www.prepody.ru/ipb.html?act=boardrules, смотрите http://www.reshebnik.ru/solutions/5/
Автор: Neolina 3.6.2009, 18:03
вообще ничего не получается =(((
решала другими методами,но преподаватель сказал что ему надо именно этими, а я их не понимаю!
Автор: venja 4.6.2009, 12:06
1) y'=(7x+2y-1)/(8x-3y+2) Методом Вариации и Бернулли
2) y"=y' * lny'/y С заменой на y'
3) y"+(x-3)y'=0 С заменой на y'
4) (x+15)y"(x)+7y'(x)+8y(x)=14 y(0)=1, y'(0)=2 По методу Маклорена, первые четыре члена.
Пожалуйста помогите....
1. Это уравнение вида
y'=f( (ax+by+c)/(dx+ey+f) ).
Оно сводится к однороднородному уравнению. Как - посмотрите в примерах или теории .
2. Ищется y' как функция у: y'=p(y). Дальше - посмотрите в примерах или теории .
3. Пусть y'=z(x). Тогда относительно z получаем простое уравнение (линейное однородное)
z'+(x-3)z=0
4. Из уравнения находите значения в нуле второй и третьей производной - подставляйте в ряд Маклорена.
Автор: Neolina 4.6.2009, 14:02
спасибо огромное)буду пытаться)
Автор: tig81 6.6.2009, 11:20
Проверьте пожалуйста уравнение!!
Откуда в 5 строчке взялся х (скобка (х-3) на него умножается)?
в ответе должна быть функция у , а не ее производная.
Автор: Neolina 6.6.2009, 11:34
А второе мне надо было Вариации и Бернулли,но похоже это совсем другой метод?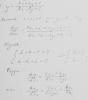
Откуда в 5 строчке взялся х (скобка (х-3) на него умножается)?
в ответе должна быть функция у , а не ее производная.
Да я умножала...
И как записать ответ?
Автор: tig81 6.6.2009, 11:36
Да я умножала...
а на каком основании вы умножили только правую часть на х?
До ответа еще далеко. Надо найти y', а затем еще раз проинтегрировав, и у.
Автор: Neolina 6.6.2009, 12:03
тогда может так?
z'+(x-3)z=0
z(x)= C индекс 1 (-x^3)+3x^2
y'=C индекс 1 (-x^3)+3x^2
y=C индекс 1 (-x^4/4)-2x^3+C индекс 2
Автор: tig81 6.6.2009, 12:08
тогда может так?
z'+(x-3)z=0
еще раз правильно разделите переменные, т.к. у вас где-то пропало dx.
Достаточно написать С1.
Автор: Neolina 13.6.2009, 14:49
Подскажите пожалуйста!
y"=y' * ln y'/y
y'=p(y)
y"=dy'/dx=dp(y)/dx=dp(y)/dy * dy/dx=p' * y'=p'p
p'p=p lnp/y
p'=ln p/y - однородное уравнение
p/y=U(y) ; p=Uy ; p'=U'y + u
U'y + U = lnU
U'y= lnU-U
du/dy * y=lnU-U
S du/lnU-U=S dy/y ; где S-интеграл
что дальше скажите пожалуйста?
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)