Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Ряды _ Область сходимости для ряда Тейлора
Автор: Fire_Inside 31.5.2009, 6:16
Здравствуйте! Задание следующее: Разложить функцию в ряд Тейлора в окрестности точки x=0 и найти область сходимости полученного ряда. Функция:
y= 1/sqrt(4-x^2)
Беру первые несколько производных, нахожу первые коэффициенты для ряды, получаю ряд. Проблема в том, что затрудняюсь определить формулу n-го члена ряда, который нужен для исследования на сходимость...
Эскизы прикрепленных изображений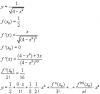
Автор: venja 31.5.2009, 7:51
Цитата(Fire_Inside @ 31.5.2009, 12:16) 
Здравствуйте! Задание следующее: Разложить функцию в ряд Тейлора в окрестности точки x=0 и найти область сходимости полученного ряда. Функция:
y= 1/sqrt(4-x^2)
Беру первые несколько производных, нахожу первые коэффициенты для ряды, получаю ряд. Проблема в том, что затрудняюсь определить формулу n-го члена ряда, который нужен для исследования на сходимость...
y= 1/sqrt(4-x^2)=(1/2)*(1-(x/2)^2)^(-1/2)
Нужно взять готовое разложение по степеням х функции (1+x)^m, затем подставить в него m=-1/2,
а вместо х подставить -(x/2)^2 (не забыть потом умножить на 1/2)
Автор: tig81 31.5.2009, 7:56
http://e-science.ru/forum/index.php?showtopic=12868&hl=
Автор: Fire_Inside 31.5.2009, 8:58
Цитата(tig81 @ 31.5.2009, 13:56)
http://e-science.ru/forum/index.php?showtopic=12868&hl=
Спасибо, уже разобрался...Это тоже мой топик был на e-science)
А 1/2 можно вообще вынести за знак суммы ряда...
Автор: tig81 31.5.2009, 10:08
Цитата(Fire_Inside @ 31.5.2009, 11:58)
Спасибо, уже разобрался...Это тоже мой топик был на e-science)
я догадалась, что ваш
Цитата
А 1/2 можно вообще вынести за знак суммы ряда...
можно
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)