Версия для печати темы

Автор: kurtz 20.4.2009, 16:54

Проинтегрировать уравнения. При заданном начальном условии найти соответствующий частный интеграл или частное решение.
1. y'+x*(y^1/3)=3y;
2. y"+y'*tgx=sin2x.
Посоветуйте как начинать решение.

Автор: Dimka 20.4.2009, 17:02

С просмотра примеров решения задач
1. Уравнение Бернулли
2. Подстановка y'=p

Автор: kurtz 20.4.2009, 19:01

1. а ничего что после равно стоит "y" а не "x"?
2. y'=p
p'+p*tgx=sin2x
p=u*v
p'=u'*v+u*v'
u'*v+u*v'+u*v*tgx=sin2x
u'*v+u(v'+v*tgx)=sin2x
v'+v*tgx=0
dv/dx=-v*tgx
dv/v=-tgx dx
Ln v=Ln cosx
v=cosx
u'*cosx+u*(-sinx)+u*cosx*tgx=sin2x
u'cosx=2sinx*cosx
u'=2sinx
du/dx=2sinx
du=2sinx dx
u=-2cosx
p=u*v=-2cosx*cosx=-2cos^2(x)
y'=p=-2cos^2(x)
dy/dx=-2cos^2(x)
dy=-2cos^2(x)dx
y=-(sin(2x)+2x)/2 — это и будет окончательный ответ?это будет частным интегралом?

Автор: Dimka 20.4.2009, 19:13

u=-2cosx+C1
p=u*v=(C1-2cosx)*cosx=C1cosx-2cos^2(x)
y'=p=C1cosx-2cos^2(x)
dy/dx=C1cosx-2cos^2(x)
dy=[C1cosx-2cos^2(x)]dx

Дальше посчитаете интеграл

y=......+С2

Дальше нужно будет найти С1 и С2, используя начальные условия, которые должны быть заданы!

Автор: kurtz 21.4.2009, 14:24

а если в условии больше ничего не дано кроме того что я уже написал в первом посте? как быть ?

Автор: Dimka 21.4.2009, 15:10

Тогда ищется общее решения
y=int [C1cosx-2cos^2(x)]dx+C2

Автор: kurtz 21.4.2009, 16:56

y=(C1*2sinx-sin2x-2x)/2 - верно? это мы проинтегрировали уровнение и нашли общее решение так?

Автор: Dimka 21.4.2009, 19:04

верно

Автор: kurtz 27.4.2009, 15:35

Помогите с первым уравнением:
1. y'+x*(y^1/3)=3y;
Заменял y=u*v но ничего путного не вышло...может все таки другой способ решения есть?

Автор: Dimka 27.4.2009, 16:20

Приведите что у Вас получилось.

Автор: kurtz 27.4.2009, 16:39

(du/dx)*v+(dv/dx)*u+x*sqrt^3(u*v)-3*u*v=0

Автор: Dimka 27.4.2009, 17:33

y'+x*(y^1/3)=3y

y'-3y=-x*(y^1/3)
y=uv, y'=u'v+v'u
u'v+v'u-3uv=-x*(uv)^(1/3)
u'v+u(v'-3v)=-x*(uv)^(1/3)
(v'-3v)=0, v=e^(3x)

u' e^(3x) =-x*(u)^(1/3)* e^(x)

du/(u)^(1/3) = -xe^(-2x) dx

3/2*(u^2/3)=e^(-2x)*(2x+1)/4+C1

u^(2/3)=e^(-2x)*(2x+1)/6+C
u=[e^(-2x)*(2x+1)/6+C]^(3/2)

y=u*v=[e^(-2x)*(2x+1)/6+C]^(3/2)*e^(3x)

Автор: Dimka 29.4.2009, 16:24

Я там одну оплошность с С1 допустил, поэтому привожу вверху полное решение.

Автор: kurtz 29.4.2009, 16:59

это так понимать?

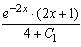
Автор: Dimka 29.4.2009, 17:03

[ e^(-2x)*(2x+1)/4] +C1