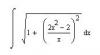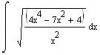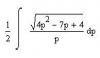Версия для печати темы

Автор: ылм 14.4.2009, 20:26

Помогите, пожалуйста решить интеграл, а то я не могу найти способа и зарываюсь так глубоко, что потом не вылезти(


Эскизы прикрепленных изображений

Автор: tig81 14.4.2009, 20:33

Откуда такой интеграл получили?

Автор: ылм 14.4.2009, 20:39

Он нужен для того, чтоб посчитать длину дуги. Просто подставил данные в формулу:


Прикрепленные изображения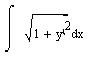

Автор: tig81 14.4.2009, 20:49

Цитата(ылм @ 14.4.2009, 23:39)

Автор: ылм 14.4.2009, 20:53

вычислить длину дуги кривой, заданной уравнением в прямоугольной системе координат
у=х^2 - 2*ln(x)
1=<x=<2

формула для вычисления длины дуги - см. рисунок
где у' - производная по х


Прикрепленные изображения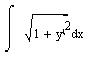

Автор: tig81 14.4.2009, 21:25

Цитата(ылм @ 14.4.2009, 23:53)

Автор: ылм 15.4.2009, 11:18

про то, что интеграл должен быть определенным - я знаю, но дело в том, что, решив неопределенный интеграл, посчитать определенный - труда не составляет)
а у'=2*x-(2/x)

Автор: Ярослав_ 15.4.2009, 14:19

Цитата(ылм @ 15.4.2009, 15:18)

Автор: ылм 15.4.2009, 15:07

Автор: Dimka 15.4.2009, 15:56

теперь подставляйте в формулу с корнем

Автор: ылм 15.4.2009, 15:57

Подставляю, и получается интеграл, который не получается решить


Эскизы прикрепленных изображений

Автор: Dimka 15.4.2009, 16:02

неправильно преобразовали.
sqrt(1+ [2x-2/x]^2 ) дальше приведите к общему знаменателю.

Автор: ылм 15.4.2009, 16:14

сделал. что дальше?

Автор: Dimka 15.4.2009, 16:18

Теперь нужно раскрыть скобки и привести к общему знаменателю

Автор: ылм 15.4.2009, 16:23

До этого я уже доходил, а дальше что?

Автор: Dimka 15.4.2009, 16:29

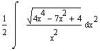
Уже лучше. Теперь нужно x из од корня вынести и внести x^2 под знак дифференциала.

Автор: ылм 15.4.2009, 16:35

готово

Автор: Dimka 15.4.2009, 16:36

теперь обозначение х^2=p

Автор: ылм 15.4.2009, 16:45

да.


Эскизы прикрепленных изображений

Автор: Dimka 15.4.2009, 16:46

Да.

Теперь подстановка t+2p=sqrt(4p^2-7p+4)

Автор: ылм 15.4.2009, 16:52

тут чего-то я не понимаю. t - это что?

Автор: Dimka 15.4.2009, 16:54

Это новая переменная. Дальше нужно возвести обе части равенства в квадрат, выразить p, найти dp=.....dt и подставить.

Автор: ылм 15.4.2009, 17:04

dp = (4t^2+14t-16)/(16t^4+56t^2+49) dt - так?

Автор: Dimka 15.4.2009, 17:07

Цитата(ылм @ 15.4.2009, 21:04)

Автор: ылм 15.4.2009, 17:17

да - р=(4-t^2)/(4t+7) , тогда dp = (-4t^2-14t-16)/(16t^2+56t+49) dt

Автор: Dimka 15.4.2009, 17:29

Только немного преобразовать придется
р=(4-t^2)/(4t+7)
dp = -2*(2*t^2+7*t+8)/(4*t+7)^2 dt

теперь подсталяйте все в исходный интеграл.

Автор: ылм 15.4.2009, 17:43

-integral{ [(2t^2+76+8)^2] / [-56t^3-t^2+224t+196] dt } верно?

Автор: Dimka 15.4.2009, 17:47

В знаменателе ошиблись.
В числителе не 76, а 7t

Автор: ылм 15.4.2009, 18:14

чего-то со знаменателем не получается.

в исходный 0,5*integral( sqrt[4p^2 -7p +4]/p dp ) подставляю р, получаю



Эскизы прикрепленных изображений

Автор: Dimka 15.4.2009, 18:30

Вторая строчка, первый интеграл. Почему знаменатель такой получился. Должен быть (4-t^2)(4t+7)(4t+7)=(4-t^2)(4t+7)^2
В конечном итоге получается

-(2t^2+76+8)^2/[(4-t^2)(4t+7)^2]
или
(2t^2+76+8)^2/[(t-2)(t+2)(4t+7)^2]

Далее выделяйте целую часть и раскладывайте на прстые дроби методом неопределенных коэффициентов

Автор: ылм 15.4.2009, 18:34

Спасибо большое за помощь)

Автор: Dimka 15.4.2009, 18:42

Там после разложения получите дробь

1/4-(15/4)/(4*t+7)^2+(7/2)/(4*t+7)+1/(t-2)-1/(t+2)

дальше нужно будет вернуться к p, затем к x и подставить пределы интегрирования по области x. Или пределы интегрирования пересчитать в пределы интегрирования по области t и вычислить длину дуги.

Автор: ылм 15.4.2009, 19:25

Спасибо еще раз) Все понятно объяснили. Завтра отпишусь о результатах.

Автор: ылм 16.4.2009, 20:33

Спасибо!!! Все досчитал, получилось) Но ответ длиннющий...