Версия для печати темы

Автор: misha_nick 22.2.2009, 21:30

Задание:Найти общее решение ДУ

Решение:
заменим y'=z значит y"=z'
получим

z'=dz/dx следовательно

тут возникают непонятки дальше то что

Автор: tig81 22.2.2009, 22:23

Если я не ошибаюсь, то в этом случае надо делать замену y'=p(y), тогда y''=p*dp/dy.

Автор: Руководитель проекта 23.2.2009, 6:08

Не ошибаетесь

Автор: Ярослав_ 23.2.2009, 7:33

Такую замену делают, когда самой функции у(х) не присутствует в уравнении.

Автор: misha_nick 23.2.2009, 7:36

получим

Далее нужно видимо разделить переменные, но как разделить р(у) - не знаю

Автор: Тролль 23.2.2009, 8:35

Получим
2p dp/(p^2 + p^4) = -dy/y

Автор: misha_nick 23.2.2009, 8:51

Интегрируем

теперь вместо р нужно подставить у' ? Верно?

Автор: misha_nick 23.2.2009, 9:42

Сначала выразим р:
[attachmentid=1382]

Подставим: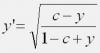


А дальше как решать

Автор: Тролль 23.2.2009, 12:02

ln (p^2/(p^2 + 1)) = -ln y + C1
p^2/(p^2 + 1) = C1/y
1 - 1/(p^2 + 1) = C1/y
1/(p^2 + 1) = 1 - C1/y
p^2 + 1 = y/(y - C1)
p^2 = y/(y - C1) - 1
p^2 = C1/(y - C1)
p = +- (C1/(y - C1))^(1/2)

Автор: misha_nick 23.2.2009, 17:24

Ах, вон чего!!!

...отлично, мы получили выражение

Дальше нужно будет заменить переменную р = y' ? Так? ... или нет...

Автор: tig81 23.2.2009, 17:32

Совершенно верно, делаем обратную замену.

Автор: misha_nick 23.2.2009, 17:37

... и получаем выражение вида

у' = +- (C1/(y - C1))^(1/2)

где у'=dy/dx верно?

dy/dx = +- (C1/(y - C1))^(1/2)

здесь нужно разделить переменные (у - влево, dx - вправо) Так?

Автор: tig81 23.2.2009, 17:39

точно

Автор: misha_nick 23.2.2009, 17:56

далее



правильно?

Автор: tig81 23.2.2009, 18:04

Вроде да. Только +С забыли да еще корень из с1 можно обозначить, например, как с2.

Автор: misha_nick 23.2.2009, 18:10

Значит выражение

можно считать общим решением данного ДУ?

Автор: tig81 23.2.2009, 18:13

Думаю, что можно.

Автор: misha_nick 23.2.2009, 18:19

Урррррраааа!!!!!

Спасибо ВАМ tig81 и Тролль!

Автор: tig81 23.2.2009, 18:22