Версия для печати темы

Автор: misha_nick 21.2.2009, 14:58

Задача: Вычислить объем тела, ограниченного заданными поверхностями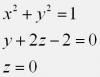

Решение: из двух последних уравнений получим, что 0<=z<=1-y/2
Найдем предел интегрирования по х и у: х^2+y^2=1
Перейдём к цилиндрическим координатам: x=r*cos fi, y=r*sin fi, z=z
Тогда х^2+y^2=r^2*cos^2 fi + r^2*sin^2 fi = r^2/
Получили пределы: 0<=r<=1 0<=fi<2pi
Отсюда получим:
[attachmentid=1360]

Проверьте пожалуйста решение.

Автор: Ярослав_ 21.2.2009, 16:02

Похоже верно.

Автор: misha_nick 21.2.2009, 16:39

Кстати, никто не поможет сделать схематичный чертёжик?

Автор: граф Монте-Кристо 21.2.2009, 16:42

Это будет прямой цилиндр,рассечённый 2мя плоскостями - перпендикулярной образующим и проходящей под углом к ним.

Автор: Ярослав_ 21.2.2009, 16:56

http://www.radikal.ru

Автор: misha_nick 21.2.2009, 17:23

Ну что ж, теперь всё ясно. Всем спасибо!

пы.сы. Ярослав_, а как называется прога, в которой ты выполнил 3D чертёж?

Автор: Ярослав_ 22.2.2009, 7:38

mathematica 6.0
Вообще, любой матпакет в силе это сделать. Даже Икселька.

Автор: olgayrevna 2.4.2010, 20:31

x^+y^2=r^2-это понятно!
А пределы как находим?