Версия для печати темы

Автор: misha_nick 16.2.2009, 19:23

Задача: Вычислить объем тела, образованного вращением вокруг оси Ох кривой L:
x-y^2=0, x=0, y=1

Решение: Так как вращение фигуры происходит вокруг оси ОХ, то объем тела определяем по формуле,



Из условия f(x)=sqrt[x], a=0, b=1.

Подставляя данные в выражение получаем


Вопрос: всё ли правильно или я где-то ошибаюсь??? (как-то просто всё получилось)

Автор: Руководитель проекта 16.2.2009, 19:38

Похоже на правду.

Автор: граф Монте-Кристо 16.2.2009, 19:54

А по-моему,то,что Вы нашли - это будет что-то вроде полости в теле.Там ведь задано ещё y=1.Или должно быть x=1?

Автор: misha_nick 16.2.2009, 20:07

Я потому и написал сюда, т.к. решение вызывает у меня сомнения и решил спросить совета у профессионалов. Укажите на неточность в решении или подскажите саму суть, а дальше я уж сам разберусь .

Автор: misha_nick 16.2.2009, 20:35

граф Монте-Кристо, кажется ты прав. Смотрим на график: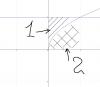


По моим вычислениям мы найдём объем области 2, а нужно - 1. Кто мне подскажет как это сделать? Формулу али ссылочку дайте плиззз!

Автор: Руководитель проекта 16.2.2009, 20:37

Упс. И не обратил внимание
Тогда интеграл надо брать от функции 1-x.

Автор: misha_nick 16.2.2009, 20:47

Чёт не понял куда 1-x вставлять.

Так

Опять 25! Чёт не то

Автор: misha_nick 17.2.2009, 19:08

У кого какие соображения на этот счёт???

Автор: Тролль 17.2.2009, 20:50

Ну да, правильно.

Автор: misha_nick 17.2.2009, 20:54

Вы уверены что решение в Сообщение #7 правильное???

Автор: Тролль 18.2.2009, 9:15

См. выше.

Автор: misha_nick 18.2.2009, 19:19

То есть, задача решена верно? Тогда буду оформлять работу. Всем отписавшимся спасибо