Версия для печати темы

Автор: Roxie Ph. 13.2.2009, 8:53

найти наибольшее значение функции y=3sin(x)+4cos(x)
понятно, что мн-во зн. 3sin(x) это [-3;3] а 4cos(x) - [-4;4]
как их сложить??

Автор: tig81 13.2.2009, 9:06

Запишем интервалы в виде двойных неравенств:
-3<=3sin(x)<=3
-4<=4cos(x)<=4
Теперь складываем эти неравенства почленно.

Автор: Ярослав_ 13.2.2009, 9:08

Про вспомогательный угол слышали? http://www.pm298.ru/trigon4.shtml

Автор: tig81 13.2.2009, 9:16

Хм... получается, что интервал [-5; 5].

Автор: Тролль 13.2.2009, 9:36

Агамс, от -5 до 5.

Автор: tig81 13.2.2009, 9:51

А из того,что я предложила, этого не получается. Не соображу, что я делаю не так.

Автор: Roxie Ph. 13.2.2009, 10:24

как вы это получили?? какую формулу использовали ?

ничего не слышала про вспомогательный угол((

Автор: Ярослав_ 13.2.2009, 10:30

По ссылке выше пройдите, там формула есть Asin(x)+Bcos(x)

Автор: Roxie Ph. 13.2.2009, 10:49

а что такое фи нулевое?? там где (x+..)

Автор: tig81 13.2.2009, 10:55

там ниже описано

Автор: Roxie Ph. 13.2.2009, 11:07

я вижу, а вычислить как?

Автор: tig81 13.2.2009, 11:13

Ну из приведенных соотношений можно получить, что ф0=arctgB/A. Но для данной конкретной задачи он вам не нужен, т.к. вам надо только получить оценку. В итоге получается 5*siny, а эта величина лежит на интервале [-5; 5]. Угол ф0 здесь не используется.

Автор: Roxie Ph. 13.2.2009, 19:32

ааа ясно, спасибо))))
а такое задание: y=sin(x)*cos(x)
(найти наибольшее значение)

Автор: tig81 13.2.2009, 19:41

пожалуйста

А где свои идеи? Распишите произведение через сумму и посмотрите, что у вас получится.

Автор: Тролль 13.2.2009, 19:55

А еще лучше это выражение домножить на 2 и на 1/2 и посмотреть, что получится.

Автор: tig81 13.2.2009, 20:02

Точно. Результат один и тот же, а получен проще.

Автор: Roxie Ph. 13.2.2009, 20:09

через сумму чего?

ааа, там 0,5 получается?

Автор: tig81 13.2.2009, 20:10

тригономнтрических функций. http://www.pm298.ru/trigon5.shtml
Но лучше воспользуйтесь советом, который дал Тролль, там лишь формулу синуса двойного угла надо знать.



это наибольшее...

Автор: Roxie Ph. 13.2.2009, 20:19

по заданию как-раз наибольшее надо было)
спасибо, Тролль)

ещё одно)
в выражении y=sqrt2(sin2x-cos2x)
получилось sqrt2*sin2x-sqrt2=y, но по-моему это неправильно((
надо найти наименьшее значение

Автор: tig81 13.2.2009, 20:28

действительно, невнимательно прочитала.

согласна

Как такое получили?

Возможно, опять не самый простой путь, но запишите cos2x как sin(Pi/2-2x) и примените формулу разности синусов

Автор: Roxie Ph. 13.2.2009, 20:37

получилось y=sqrt2(2cosPi*sin[(-Pi\2-4x)\2]

Автор: tig81 13.2.2009, 20:39

У меня не так получилось, подробнее можно?!

Автор: Ярослав_ 14.2.2009, 10:24

Можно так:
sqrt(2)*[sqrt(2)*[sin(2x)-cos(2x)]/sqrt(2)];
2*[cos(pi/4)sin(2x)-sin(pi/4)cos(2x)];
2sin(2x-pi/4)

Автор: tig81 14.2.2009, 10:27

Автор: Георгий 24.2.2009, 12:46

А посмотрите-ка на график! Вдруг наврали что-либо?


Эскизы прикрепленных изображений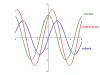

Автор: Тролль 24.2.2009, 14:24

Кто наврал и где?