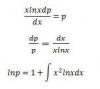Версия для печати темы

Автор: Wave 12.12.2008, 8:40

Найти общее решение: y''xlnx-y'=0
монжо так?: k^2 *xlnx-k=0
k(первая, вторая)=0, k=1/(xlnx)
Y1=e^0=1; Y2=xe^0=x
Y00=C1+xC2 ???

Автор: tig81 12.12.2008, 9:19

Мне кажется, здесь нужно сделать замену: y'=p, тогда получаем уравнение xlnxp'-p=0, а это уже ДУ первого порядка с разделяющимися переменными.

Автор: граф Монте-Кристо 12.12.2008, 9:20

Нет,так нельзя.
Сделайте замену y'(x)=z(x),тогда степень понизится,можно будет разделить переменные и проинтегрировать.

P.S.: Эх,чуток совсем не успел

Автор: Wave 12.12.2008, 9:38

p'-p/xlnx=0
а потом через: p=uv?

Автор: tig81 12.12.2008, 17:22

Лучше используйте тот факт, что получено http://www.reshebnik.ru/solutions/5/1/.

Автор: Wave 16.12.2008, 20:48

Автор: Ярослав_ 16.12.2008, 21:04

p'-p/xlnx=0;
dp/p=dx/(x*ln(x));
Ln(p)=Ln[Ln(x)];
p=Ln(x)

Автор: Wave 16.12.2008, 21:19

y=xlnx-x

в задаче надо найти общее решение это: y=xlnx-x+C ?

Автор: Ярослав_ 16.12.2008, 21:38

Верность решения можно проверить, если подставить y'' и y' в уравнение y''xlnx-y'=0 .

Автор: Wave 16.12.2008, 21:47

а общее: y=xlnx-x-2 ?

Автор: Wave 17.12.2008, 8:27

? так/нет

Автор: Ярослав_ 17.12.2008, 8:39

Нигде не нашел, что нужно частное решение. Судя по всему, оно такое у(0)=1?
Тогда вроде верно.

Автор: Wave 17.12.2008, 8:56

ну надо же общее оно с "С" получается :y=xlnx-x+C ?

Автор: граф Монте-Кристо 17.12.2008, 9:22

У Вас уравнение второй степени,следовательно,должно получиться 2 константы.

Автор: Wave 17.12.2008, 9:46

а где вторую то взять?

в ln|x+C| ?

Автор: граф Монте-Кристо 17.12.2008, 20:53

Когда Вы ищете p,у Вас получилось:

Потом вспоминаете,что p=y', и находите у(х).Получится как раз две константы.

Автор: Wave 24.12.2008, 7:49

y=C_1*xlnx-x+C_2 вот так?

Автор: граф Монте-Кристо 24.12.2008, 8:04

По идее,так.