Версия для печати темы

Автор: kaskara 30.10.2008, 12:11

Добрый вечер! Помогите построить график в XYZ координатах, если известна такая зависимость Z=XY. Спасибо за внимание!

Автор: Тролль 30.10.2008, 12:52

Получается гиперболический параболоид.

http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%D0%B2%D0%B5%D1%80%D1%85%D0%BD%D0%BE%D1%81%D1%82%D1%8C_%D0%B2%D1%82%D0%BE%D1%80%D0%BE%D0%B3%D0%BE_%D0%BF%D0%BE%D1%80%D1%8F%D0%B4%D0%BA%D0%B0

Автор: kaskara 30.10.2008, 15:46

Может вопрос не уместен, но если построить поверхность уравнения PV=T в координатах (P,V,T) - такой же график будет - гиперболический параболоид или надо учитывать законы Физики?

Автор: граф Монте-Кристо 30.10.2008, 16:00

Видимо да,только придётся ограничиться только той частью поверхности,где P>0 и V>0.

Автор: kaskara 31.10.2008, 3:01

"Тролль
сообщение Вчера, 17:52
Сообщение #2

Получается гиперболический параболоид.

http://ru.wikipedia.org/wiki/%D0%9F%D0%BE%...%B4%D0%BA%D0%B0 "

Обьясните как его построить, какие где расположены оси? на рисунке не видно названия осей. И помоему это уравнение гиперболического параболоида:

\frac{x^2}{a^2}-\frac{y^2}{b^2}=2pz\!

совсем не похоже на мое z=xy. в моем уравнении если вы заметили нет никаких квадратов и тем более разности дробей. Обоснуйте свой ответ. Докажите расчетами что z=xy - гиперболический параболоид.

Заранее большое спасибо!

Автор: Тролль 31.10.2008, 5:45

Делается следующая замена (переходим к новой системе координат)
x = x1 + y1
y = x1 - y1
Тогда
z = x * y = (x1 + y1) * (x1 - y1) = (x1)^2 - (y1)^2

Автор: kaskara 6.11.2008, 7:54

Все же я думаю, что надо учитывать параметры. например : мне надо построить поверхность по формуле менделеева-клапейрона PV=RT, где R- константа значит уравнение примет вид PV=T отсюда следует что должен получиться гиперболический параболоид, но если вы знаете из этой формулы вытекают много законов для: изохорного процесса, изобарного, изотермического, адиабатного, политропного, вот у этих процессов есть графики 2D - прямая, прямая, гипербола и т.д. если это учитывать то график никак не будет гиперболическим параболоидом...

Выложи пожалуйста все расчеты по которым будет видно, что, откуда и куда подставили, и по каким точкам построен график... мне надо обьяснять будет преподавателю как я его построил и почему именно такая поверхность получилась, не скажу же что на форуме сказали! Спасибо большое за помощь! Жду конкретного примера! Спасибо за внимание!

Автор: Тролль 6.11.2008, 8:20

При изохорных и иных процессах одна из переменных V, P или T будет константой, тогда графика указанного процесса будет представлять собой сечение плоскостью этого самого гиперболического параболоида. Его сечениями как раз и будут прямые и гиперболы.

Автор: kaskara 6.11.2008, 11:45

А у тебя нет наглядных примеров? Пожалуйста поделись если есть буду очень благодарен!

А как насчёт вот такой поверхности? Если смотреть с каждой стороны, то как раз можно разглядеть прямые и гиперболу!

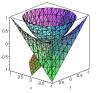
если x и y заменить на pv, а ось z (вертикальная) на T, то тогда вроде график очень близок к правде

Автор: Тролль 6.11.2008, 12:14

Зато на гиперболический параболоид не похоже. А z = xy - это гиперболический параболоид. Можно в какой-нибудь программе построить, которая строит трехмерные графики.

Автор: Ярослав_ 6.11.2008, 12:38

У меня такое строит.

http://radikal.ru/F/s41.radikal.ru/i091/0811/69/96aa71a283fd.jpg.html


http://radikal.ru/F/s39.radikal.ru/i083/0811/4f/c0a60e5570f2.jpg.html

Автор: Тролль 6.11.2008, 12:45

Похоже на правду

Автор: kaskara 6.11.2008, 13:13

Ну спасибо всем за помощь! Вроде разобрался что к чему...
Ярослав_ спасибо за изображения!
Тролль и граф Монте-Кристо спасибо за объяснения!

P.S. если чего не додумаю, спрошу