Версия для печати темы
Нажмите сюда для просмотра этой темы в обычном формате
Образовательный студенческий форум _ Пределы _ lim(X->a)(cosx*ln(x-a))/ln(e^x-e^a)
Автор: MalStr 21.10.2008, 7:32
Решите Плиз предел! неделю над ним мучался! ниче не выходит!
lim (cosx*ln(x-a))/ln(e^x-e^a) ; X->a
Автор: tig81 21.10.2008, 7:36
http://www.prepody.ru/ipb.html?act=boardrules
Что делали, что получили?
http://ru.wikipedia.org/wiki/%D0%9F%D1%80%D0%B0%D0%B2%D0%B8%D0%BB%D0%BE_%D0%9B%D0%BE%D0%BF%D0%B8%D1%82%D0%B0%D0%BB%D1%8F
http://www.toehelp.ru/theory/math/lecture08/lecture08.html
Автор: MalStr 21.10.2008, 7:46
здоровенное уравнение выходит если сразу производную находить и толку никакого! наверкняка надо какие-нибудь преобразования с натур логарифмами сделать
вторую производную тож пробовал! ничего!
Автор: tig81 21.10.2008, 7:54
Заменой x-a=t можно свести к пределу при t->0, и тогда воспользоваться тем, что ln(1+x) эквивалентно х при х->0. Надо посмотреть, что все это даст
Автор: MalStr 23.10.2008, 7:07
Вообщем получилось что-то, но уверен что правильно! а если правильно то уверен можно было сделать проще. проверьте пожалуйста!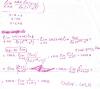
Автор: Тролль 23.10.2008, 7:25
Ужас как сложно)
ln (e^(t + a) - e^a) = ln (e^a * (e^t - 1)) = ln e^a + ln (e^t - 1) =
= a + ln (e^t - 1)
e^t - 1 эквивалентно t
Получаем lim (t->0) ln t/(a + ln t) = lim (t->0) 1/(a/ln t + 1) = 1.
Автор: MalStr 23.10.2008, 7:34
а почему e^t-1 эквивалентно t?
Автор: Тролль 23.10.2008, 7:35
Потому что (e^t - 1)/t -> 1 при t -> 0
Автор: MalStr 23.10.2008, 7:40
наверное я что-то не понимаю! это ж 0 на 0 стремиться к 1?
Автор: Тролль 23.10.2008, 7:48
Похоже вообще ничего не понимаете.
sin x/x -> 1 при x -> 0 (здесь тоже 0 на 0)
Автор: MalStr 23.10.2008, 7:51
так этож замечат предел))! пасиб вообщем!
Автор: tig81 23.10.2008, 8:01
наверное я что-то не понимаю! это ж 0 на 0 стремиться к 1?
Посмотрите http://matclub.ru/doc/ekvival.doc или http://elib.ispu.ru/library/math/sem1/index.html
Автор: MalStr 24.10.2008, 7:37
проверьте еще , пожалуйста, один пример!
Эскизы прикрепленных изображений
Автор: Тролль 24.10.2008, 9:09
Вроде правильно. Только, по-моему, второй раз Лопиталя применять не нужно, потому что числитель стремится к 0, а знаменатель к бесконечности.
Автор: venja 24.10.2008, 12:58
второй раз Лопиталя применять не нужно, потому что числитель стремится к 0, а знаменатель к бесконечности.
Кстати, применение правила Лопиталя при отсутствии неопределенности может привести к неверному результату.
Русская версия Invision Power Board (http://www.invisionboard.com)
© Invision Power Services (http://www.invisionpower.com)
