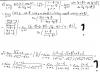Версия для печати темы

Автор: Motogift 19.12.2007, 13:31

Пожалуйста решите вот эти пределы:


Эскизы прикрепленных изображений

Автор: граф Монте-Кристо 19.12.2007, 14:06

Здесь Вам никт ничего просто так решать не будет.Помочь в том что не получается - другое дело,а так дело не пойдёт.

Автор: Motogift 19.12.2007, 17:37

Дак у меня и так ни чего не получается, я уже над этими пределами два дня сижу никак не могу решить, а у меня скоро зачёт, ну помогите пожалуйста чем можете, буду очень благодарен.

Автор: venja 19.12.2007, 17:55

Ко всем можно применить правило Лопиталя (уже проходили?).
Можно и по-другому, но долго объяснять.

Автор: tig81 19.12.2007, 19:27

Так два дня сидите, хоть что-то написали. Вот опишите, что сделали, мы посмотрим и исправим.

Автор: Motogift 19.12.2007, 20:40

Вот первые два, подскажите , как дальше?


Вот ещё!


Эскизы прикрепленных изображений

Автор: tig81 19.12.2007, 21:05

Ну, скажем так, это другой разговор
е) а почему домножаете на sqrt(x)-1?
Имеем неопределенность (0/0). Числитель записываем как разность квадратов, для этого числитель и знаменатель дроби домножаем на sqrt(x)+1
Аналогично, знаменатель можно привести к разности кубов, для этого домножаем числитель и знаменатель дроби на недостающую скобку ((x^(2/3))^2+x^(2/3)+1). Далее сворачиваем числитель и знаменатель, получаем limit{(x-1)((x^(2/3))^2+x^(2/3)+1)}/{(x^2-1)sqrt(x)+1}
д) далее по формулам приведения получаем, что sin(14Pi+7Piy)=sin(7Piy), аналогично для синуса в знаменателе. Затем используем тот факт, что при y->0 siny~y. Сокращаем и получаем....
в) можно, наверное, так как делаете, но лучше применить правило Лопиталя. Для этого берете производную от числителя и от знаменателя отдельно...
б) делается по аналогии с е)..

Автор: Motogift 20.12.2007, 10:27

Большое спасибо! А что такое (sqrt)

Автор: tig81 20.12.2007, 10:32

sqrt-это корень квадратный

Автор: Motogift 25.12.2007, 9:41

Помогите пожалуйста не понял как решаются вот эти пределы, правило лопиталя применять нельзя:


Эскизы прикрепленных изображений

Автор: tig81 25.12.2007, 9:51

в) теперь в числителе примените ф-лы синус суммы и косинус суммы, вместо синуса и косинуса 45 градусов подставьте их значения, ана логично в знаминателе для тангенса. Далее воспользуйтесь бесконечно малыми, т.е. при x->0 tgx~x, sinx~x
г) в числителе выделяем сумму кубов, вы чуть-чуть не на то домножаете
(x^(1/3)-1)*((x^(1/3))^2+x^(1/3)+1), т.к. ф-ла
a^3-b^3=(a-(a^2+ab+b^2), а у вас четвертая степень откуда-то. В знаминателе выделяете разность квадратов a^2-b^2, для это домнажаем на сопряженное к знаменатилю (то есть уже на сумму корней)!

Автор: Motogift 25.12.2007, 12:18

Г) у меня получилось: Lim(x-1)=(x-1)/(1-x) а дальше как?

в) получилось Lim(y-0)={((y*sqrt2/2)+(y*sqrt2/2))-((cos*sqrt2/2)-(y*sqrt2/2))}/{ln(y+1/1-y)}

Автор: tig81 25.12.2007, 13:17

Г) имеется в виду Lim(x->1)(x-1)/(1-x)? Выносим минус или в чисоителе или знаменателе и сокращаем, но непонятно, почему такое выражение получилось, а где скобка,на которую вы домнажали. Если числитель домнажается на какое-то выражение, то и знаменатель надо умножить на это же выражение (основное свойство дроби)
в) Lim(y-0)={((y*sqrt2/2)+(y*sqrt2/2))-((cos*sqrt2/2)-(y*sqrt2/2))}/{ln(y+1/1-y)}
а почему у просто? Не совсем понятно,как вы раскрывали, помоему вы немного не так ф-лу применили:
sin(x+y)=sinxcosy+cosxsiny...

Автор: Motogift 25.12.2007, 13:24

Напишите пожалуйста полностью решение, а то я чёто запутался! Буду очень благодарен!

Автор: tig81 25.12.2007, 14:02

лучше вы напишите, а я посмотрю и если что, то подкорректирую

Автор: Motogift 25.12.2007, 14:21

вот!


Эскизы прикрепленных изображений

Автор: tig81 25.12.2007, 14:33

в) до замены на бесконечно малые:
cosPi/4=sqrt(2)/2, а не эквивалентен Pi/4. Аналогично и tgPi/4=1. Подставте эти табличные значения, посмотрите,что у вас в числителе взаимно уничтожится, а затем заменяйте бесконечно малые на эквивалентные
г) например, у вас была дробь
a/b=(a*c)/(b*c) не равно (a*c)/b.
Еще раз повторяю, если вы числитель домножаете на некоторое выражение, то и знаменатель надо домножить на это же выражение; если знаменатель дроби домножить на некоторое выражение, то и числитель умножаем на это же выражение.

Автор: Motogift 25.12.2007, 15:04

Правильно? Как дальше?


Эскизы прикрепленных изображений

Автор: Motogift 25.12.2007, 15:18

и второй: ={(x^1/3-1)*((x^1/3+x^1/3+1)*(sqrt1+x+sqrt2x)}/{(sqrt1+x-sqrt2x)*(sqrt1+x+sqrt2x)*((x^1/3)^2+x^1/3+1)}={(x-1)*(sqrt1+x+sqrt2x)}/(1+x)*((x^1/3)^2+x^1/3+1)=?

Автор: tig81 25.12.2007, 15:19

похоже! в числителе раскрываем скобки и там что-то взаимно уничтожится. Затем sinx~x, tgx~x. Переписываем, что получается, а также нужно воспользоваться тем фактом, что при x->0 ln(1+x)~x, приводим логарифм к такому виду: lnx=ln(1+(x-1)). Пробуйте, если не получится пишите, посмотрим, что дальше делать

Автор: tig81 25.12.2007, 15:37

еще раз ф-лу
a^3+b^3=(a+b )(a^2-ab+b^2)
Выделяю красным,с чем не согласна
={(x^1/3-1)*((x^1/3+x^1/3+1)*(sqrt(1+x)+sqrt(2x))}/{(sqrt(1+x)-sqrt2x)*(sqrt(1+x)+sqrt2x)*((x^1/3)^2+x^1/3+1)}={(x-1)*(sqrt1+x+sqrt2x)}/(1+x)*((x^1/3)^2+x^1/3+1)
(a-b )(a+b )=a^2-b^2
Где sqrt(1+x) раставляйте скобки, а то читается как корень из 1 + х.
Пробуйте, должно сократиться и неопределенности больше нет!

Автор: Motogift 25.12.2007, 15:54

первый: ={sin*sqrt2/2+cosy*sqrt2/2-cosy*sqrt2/2+siny*sqrt2/2}/{ln(tgy+1/1-tgy)}=|siny~y,tgy~y|=
{y*sqrt2/2+y*sqrt2/2}/{ln(y+1/1-y}={y*sqrt2/2+y*sqrt2/2}/{ln(1+(y-1))=?

так: ={0}/{(1+1)*(1+1+1)}=0/6=0 ?

Автор: tig81 25.12.2007, 15:57

Раставляйте скобки, а то читать тяжело
={siny*sqrt2/2+cosy*sqrt2/2-cosy*sqrt2/2+siny*sqrt2/2}/{ln(tgy+1/1-tgy)}=|siny~y,tgy~y|=
{y*sqrt2/2+y*sqrt2/2}/{ln((y+1)/(1-y))}={y*sqrt2}/{ln((y+1)/(1-y)))={y*sqrt2}/{ln(1+(y+1)/(1-y)-1))
выделенные слагаемые приведите к общему знаменателю, это и будет ln(1+x)~x

Автор: Motogift 25.12.2007, 16:12

={siny*sqrt2/2+cosy*sqrt2/2-cosy*sqrt2/2+siny*sqrt2/2}/{ln(tgy+1/1-tgy)}=|siny~y,tgy~y|=
{y*sqrt2/2+y*sqrt2/2}/{ln((y+1)/(1-y))}={y*sqrt2}/{ln((y+1)/(1-y)))={y*sqrt2}/{ln(1+(y+1)/(1-y)-1))={y*sqrt2}/ln({(1-y)-1+(y+1)}/{(1-y)-1}=|lny=ln({(1-y)-1+(y+1)}/{(1-y)-1)~y|={y*sqrt2/2}/{y}=sqrt2/2?

Автор: tig81 25.12.2007, 17:28

Упрощаем подлогарифмическую функцию:
ln((y+1)/(1-y))=ln(1+(y+1)/(1-y)-1)=ln(1+(y+1-1+y)/(1-y))=ln(1+2y/(1-y))~2y/(1-y)
тогда искомый предел
...={y*sqrt2}/(2y/(1-y))=sqrt2*(1-у)/2=sqrt2/2
Ну и где надо lim дописываем
Смотрю, что-то подобное получалось, но потом в скобках запуталась, так что решила сама сделать

Автор: Motogift 25.12.2007, 17:32

большое спасибо!

Автор: tig81 25.12.2007, 17:42

Автор: Motogift 25.12.2007, 17:52

а второй правильно?

Автор: tig81 25.12.2007, 18:10

пропустила этот ваш ответ!
ранее было, смотрите исправляю прямо в тексте
={(x^1/3-1)*((x^2/3+x^1/3+1)*(sqrt(1+x)+sqrt(2x))}/{(sqrt(1+x)-sqrt2x)*(sqrt(1+x)+sqrt2x)*((x^1/3)^2+x^1/3+1)}={(x-1)*(sqrt(1+x)+sqrt2x)}/(1-x)*((x^1/3)^2+x^1/3+1)=
=-{(x-1)*(sqrt(1+x)+sqrt2x)}/{(x-1)*((x^1/3)^2+x^1/3+1)}=-(sqrt(1+x)+sqrt2x)/((x^1/3)^2+x^1/3+1)=-(sqrt(2)+sqrt(2))/(1+1+1)=-2sqrt(2)/3
СМотрите, где ошиблись

Автор: Motogift 25.12.2007, 18:36

Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!Спасибо!

Автор: tig81 25.12.2007, 18:50

пожалуйста^14