Образовательный студенческий форум [Русская версия Invision Power Board]

Автор: miss Pofig 10.3.2018, 8:14

Помогите пожалуйста, не понимаю, как проверить. Может решила не правильно?

Эскизы прикрепленных изображений

Автор: tig81 10.3.2018, 9:31

Цитата(miss Pofig @ 10.3.2018, 10:14)

Помогите пожалуйста, не понимаю, как проверить. Может решила не правильно?

Ответ на вопрос: для проверки нужно полученный результат продифференцировать (найти производную)

П.С. А так лучше действительно сделать замену, а не применить метод интегрирования по частям. У Вас написано "сделаем замену", а по сути делаете другое.
П.С.1 Сделайте замену (sinx)^2=t

Автор: miss Pofig 10.3.2018, 9:59

Цитата(tig81 @ 10.3.2018, 12:31)

Ответ на вопрос: для проверки нужно полученный результат продифференцировать (найти производную)

П.С. А так лучше действительно сделать замену, а не применить метод интегрирования по частям. У Вас написано "сделаем замену", а по сути делаете другое.
П.С.1 Сделайте замену (sinx)^2=t

А если я заменю над экспонентой sin на t, не придется все равно по частям интегрировать?

Автор: tig81 10.3.2018, 10:01

Цитата(miss Pofig @ 10.3.2018, 11:59)

А если я заменю над экспонентой sin на t, не придется все равно по частям интегрировать?

Что получилось после замены?)))

Автор: miss Pofig 10.3.2018, 10:07

Цитата(tig81 @ 10.3.2018, 13:01)

Что получилось после замены?)))

Вот так. Я совсем пенек?)

Эскизы прикрепленных изображений

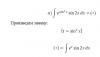
Автор: tig81 10.3.2018, 10:17

Цитата(miss Pofig @ 10.3.2018, 12:07)

Вот так. Я совсем пенек?)

не совсем, но немного есть)))

После замены старой переменной х не должно остаться.

Если (sinx)^2=t, тогда "старый дифференциал"

((sinx)^2)'dx=(t)'dt

Ищите указанные производные

Цитата(miss Pofig @ 10.3.2018, 12:07)

Вот так. Я совсем пенек?)

Посмотрите примеры:
http://ru.solverbook.com/spravochnik/integraly/metody-resheniya-integralov/
http://ru.solverbook.com/spravochnik/integraly/integrirovanie-zamenoj-peremennoj/
http://ru.solverbook.com/primery-reshenij/primery-resheniya-integralov/
http://ru.solverbook.com/primery-reshenij/primery-resheniya-neopredelennyx-integralov/

Автор: miss Pofig 10.3.2018, 10:19

Цитата(tig81 @ 10.3.2018, 13:17)

не совсем, но немного есть)))

После замены старой переменной х не должно остаться.

Если (sinx)^2=t, тогда "старый дифференциал"

((sinx)^2)'dx=(t)'dt

Ищите указанные производные
Посмотрите примеры:
http://ru.solverbook.com/spravochnik/integraly/metody-resheniya-integralov/
http://ru.solverbook.com/spravochnik/integraly/integrirovanie-zamenoj-peremennoj/
http://ru.solverbook.com/primery-reshenij/primery-resheniya-integralov/
http://ru.solverbook.com/primery-reshenij/primery-resheniya-neopredelennyx-integralov/

Вы чертов гений!!!!!!! Я 2-е суток с этим вожусь!!!!! Ночами снится)))) Я поняла. спасибо огромное!!!!

Эскизы прикрепленных изображений

Автор: tig81 10.3.2018, 10:21

Цитата(miss Pofig @ 10.3.2018, 12:19)

Вы чертов гений!!!!!!! Я 2-е суток с этим вожусь!!!!! Ночами снится)))) Я поняла. спасибо огромное!!!!

Ну теперь ПРАВИЛЬНО найти табличный интеграл (не забыть константу интрегрирования), а потом сделать обратную замену!)))

Автор: miss Pofig 10.3.2018, 10:23

Цитата(tig81 @ 10.3.2018, 13:21)

Ну теперь ПРАВИЛЬНО найти табличный интеграл (не забыть константу интрегрирования), а потом сделать обратную замену!)))

В итоге получилось так. Надеюсь, я опять не оплошала?

Эскизы прикрепленных изображений

Автор: tig81 10.3.2018, 10:25

Цитата(miss Pofig @ 10.3.2018, 12:23)

В итоге получилось так. Надеюсь, я опять не оплошала?

В проверке +С в самом начале потеряли)), но всё равно правда потом на результат не влияет, т.к. производная константы равна 0.

А так всё замечательно

Автор: miss Pofig 10.3.2018, 10:29

Цитата(tig81 @ 10.3.2018, 13:25)

В проверке +С в самом начале потеряли)), но всё равно правда потом на результат не влияет, т.к. производная константы равна 0.

А так всё замечательно

Спасибо большое за подсказку!

Автор: tig81 10.3.2018, 10:36

Цитата(miss Pofig @ 10.3.2018, 12:29)